Erdős 的三角不等式 – 搞英语 → 看世界

平面几何自古以来就被人们研究，然而几千年后，新的成果不断涌现，其中不乏优雅的结果。证明一个欧几里得不会在意的复杂定理，很容易得出一个新的结果。但更令人印象深刻的是，能得出一个欧几里得能够理解并觉得有趣的新定理。

1935 年，保罗·埃尔德什（Paul Erdős）猜想了另一个三角不等式，该不等式由 Mordell 和 Barrow 于 1937 年证明 [1]。

设P为三角形ABC内的一个点。令x , y , z为P到顶点的距离，令p , q , r为 P 到边的距离。则

x + y + z ≥ 2( p + q + r )

只有当P是等边三角形的中心时，才相等 [2]。上图中，该定理指出，蓝色虚线的总长度是红色实线的两倍多。

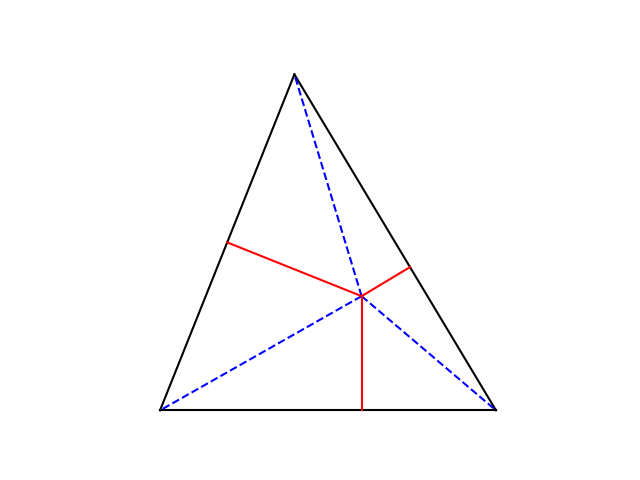
不等式的左右两边相距多远？这正是我之前那篇关于从三角形中选取随机点的文章的动机。我想生成随机点，并关注 Erdős-Mordell-Barrow 不等式的两边。

我们可以通过在三角形内生成随机点并用表示不平等差距的颜色绘制这些点来可视化不平等，深蓝色对应较大的差距。

这表明三角形中部的不平等现象比顶点附近的不平等现象更为严重。

[1] 问题 3740，美国数学月刊，44（1937）252-254。

[2] 你可以将其解释为比较重心坐标和三线坐标的定理。