在考虑如何通过对废水进行测序来识别未来的流行病时,您的目标可能是在部分人目前被感染之前发出警报。然而,您实际上能够观察到的是测序读数,从感染率中移除了几个步骤。我们是否可以使用 covid 数据来估计当前感染某种病原体的人的比例如何转化为与病原体匹配的废水测序读数的比例?
南加州废水的 RNA 病毒组学和 SARS-CoV-2 单核苷酸变异体的检测( Rothman et al 2021 ) 是我所知道的该领域最接近的研究,尽管这并不是他们想要回答的。他们采集了许多城市废水样本,提取了 RNA,对其进行过滤以增加与病毒相对应的 RNA 的比例,然后对其进行测序。
(他们还做了其他几件事,包括丰富一些呼吸道病毒样本,但这里我只看未丰富的数据。)
他们获得了 795M 的测序读数,其中 337 个被他们确定为新冠病毒。这意味着所有读取中 covid 的比例(“比例丰度”)为 4e-7。论文中有一个错字,他们说这是“0.0004%”,但我写信给作者询问,他们确认这是一个缺失的零。
在此期间有多少人被感染?回答这个问题的第一个棘手的事情是这个时期的测序数量并不统一:
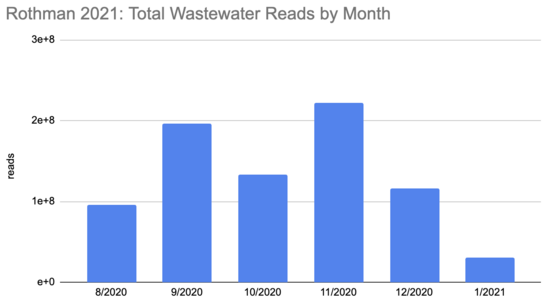
罗斯曼 2021 SF4_sample_metadata: xlsx
也不是covid案件:
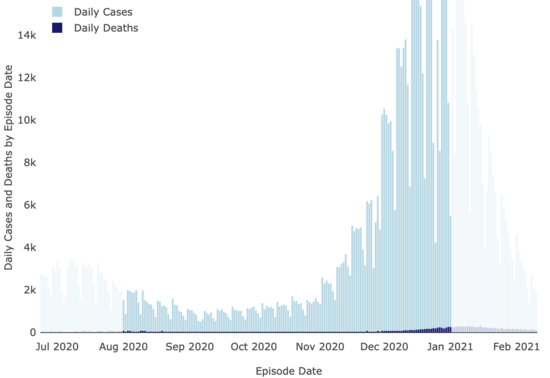
洛杉矶县Covid 仪表板
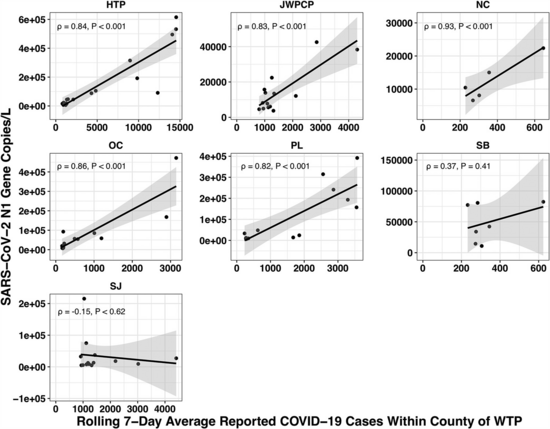
该论文通过查看该县每个水处理厂服务的病例数与他们使用 qPCR 在样本中测量的 covid 数量之间的关系来解释确诊病例的变异性。由于 qPCR 可以为您提供给定成本的更精确估计,因此他们能够量化 7 个工厂中 85 个样本的 covid 组成:
(您可能想知道:如果 qPCR 既便宜又精确,为什么不直接使用它来寻找新的流行病?为什么要在测序上投入如此多的精力和金钱?qPCR 的问题在于它是一种检查特定序列多少的方法存在于样本中。这意味着您必须已经知道要查找的内容,并且可能无法捕捉到新奇的东西。)
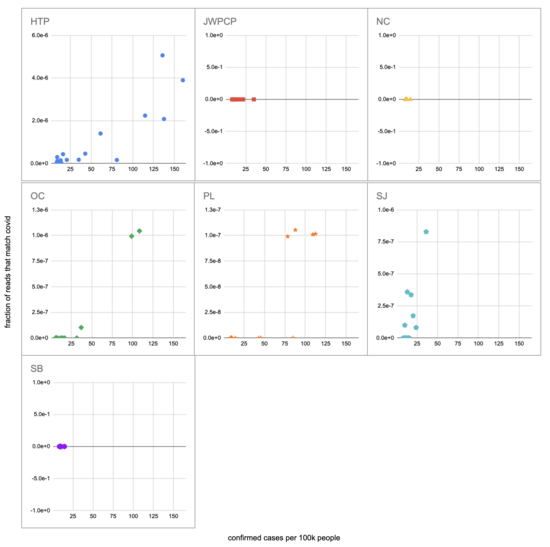
让我们重新创建此图表,但通过匹配 covid 而不是 qPCR 的读取部分进行量化。我通过寻找与 covid 的一些长度为 40 的子字符串(“40-mers”)的完全匹配来识别读取,并找到了 227(代码)。我从约翰霍普金斯大学的 CSSE 中提取了确诊病例,计算了一个以 7 天为中心的移动平均线,并将其( 代码)与示例元数据(SF4: xlsx )结合在一起。这给了我们( 工作表):
我们没有得到任何与 JWPCP、NC 或 SB 植物的 covid 匹配的读数,但这并不奇怪,因为测序不是很敏感,而且他们只在研究早期 covid 水平非常低时对这些植物进行了采样。
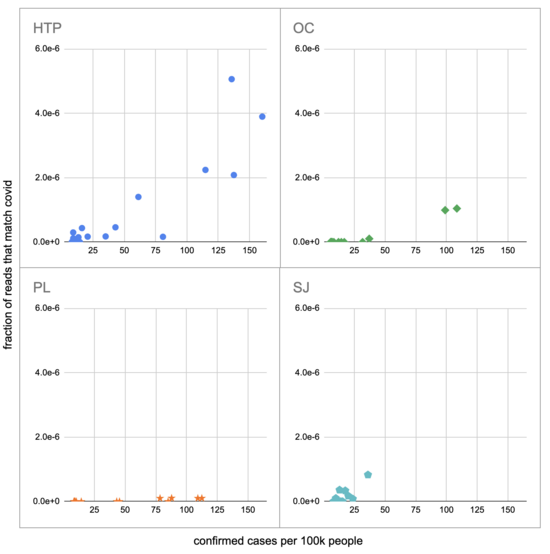
把我们确实看到covid的四种植物拿出来,结果显示出很大的可变性:
最显着的对比是在 HTP 和 PL 之间,其中有明显的积极趋势,即使比率达到每 100k 超过 100 个病例,我们每个样本的 covid 读数也从未超过一个。我们确实从 qPCR 知道 PL 的水中存在 covid,并且随着病例的增加,它的浓度也会上升,所以令人惊讶的是,我们没有得到预期的读取次数。
另一个方向也存在分歧,在 SJ qPCR 中,covid 水平没有随着病例的增加而增加,但我们确实看到了增加。然而,这种增长并不是很强劲,因为它完全由单个样本驱动,即最后一天 (2020-11-18) 的 12 个 covid 读取。
将线性模型拟合到这四个以及整个数据中,我看到:
| 植物 | 估计每 100k 读取 100 个案例 |
|---|---|
| HTP | 2.2e-6 |
| 超频 | 8.6e-7 |
| PL | 7.9e-8 |
| SJ | 1.2e-6 |
| 全部 | 1.3e-6 |
作为一个健全的检查,让我们尝试以不同的方式计算它,而不用花哨的统计数据。我们可以将 covid 读取的比例与读取加权的病例率进行比较。例如,如果我们有:
| 县 | 日期 | 总读取 | 每 10 万个案例 |
|---|---|---|---|
| 橙子 | 2020-08-12 | 2.1M | 8.4 |
| 洛杉矶 | 2020-08-12 | 5.8M | 20.0 |
| 圣地亚哥 | 2020-08-13 | 11.0M | 8.8 |
那么阅读加权的病例率,或阅读“经历”的平均病例率是:
2.1M * 8.4 + 5.8M * 20.0 + 11.0M * 8.8 -------------------------------------- 2.1M + 5.8M + 11.0M
在此示例中,每 100k 为 12.2。
计算我得到的完整数据( 代码、工作表)的读取加权平均病例率为每 100k 33 例。该论文发现 4e-7 的读取是 covid,因此按 100/33 缩放,我们可以在表中添加另一个估计:
| 植物 | 估计每 100k 读取 100 个案例 |
|---|---|
| HTP | 2.2e-6 |
| 超频 | 8.6e-7 |
| PL | 7.9e-8 |
| SJ | 1.2e-6 |
| 全部 | 1.3e-6 |
读取加权 1.2e-6
这与我们通过线性回归得到的结果非常接近,这令人放心。然而,在我们太放心之前,我们应该记住,PL 数据给出的数字要低得多。
尽管如此,让我们继续尝试预测一些当前感染者的测序读数。到目前为止,我们一直在使用确诊病例,并不是所有的感染都得到确认,甚至没有被注意到。疾病预防控制中心估计,从 2020 年 2 月到 2021 年 9 月,报告了 1:4 的感染。而且,非常粗略地说,第一次感染新冠病毒的典型未接种疫苗的人可能会被感染约 2 周。这给了我们一个 56 (4*14) 的因子和一个新表:
| 植物 | 估计每 10 万人中有 100 个当前感染者 |
|---|---|
| HTP | 3.9e-8 |
| 超频 | 1.5e-8 |
| PL | 1.4e-9 |
| SJ | 2.1e-8 |
| 全部 | 2.3e-8 |
读取加权 2.2e-8
这是一个非常粗略的估计:14天真的是典型的传染期吗?这些污水处理厂的集水区在此期间确认的感染比例真的是 1:4 吗?废水水平是否会导致确诊病例,如果是,会导致多少?为什么在 PL 测量的水平比其他地方低 20 倍?在传染期、脱落量、废水中的稳定性等方面,covid 是否与潜在的未来流行病相似?如果您尝试检测新的病原体,您会使用 Rothman 2021 中的方法吗?而且单次测序读取不足以识别大多数新型病原体,因此我在以后的处理中没有涉及到其他因素。尽管如此,运行这些计算有助于了解像这样的项目可能需要多少排序。