
四年半前,我推出了 HIBP 的 Pwned Passwords 的第 2 版,它实现了一个非常酷的 k-匿名模型,由 Cloudflare 的大脑提供。 2018 年晚些时候,我对 Mozilla、1Password 和少数其他付费用户使用的电子邮件地址搜索功能做了同样的事情。它工作得很好;它速度快、效率高,而且最重要的是,它是匿名的。然而,我不时收到这样的消息:
你为什么使用 SHA-1?它不安全且已弃用。
或者:
我们的 [插入填写文书工作但在这里没有技术理解的人的头衔] 说 k-匿名涉及向您发送 PII。
当你揭开封面并了解下面发生的事情时,这两种立场都毫无意义,但我明白这些结论是如何从表面上得出的。所以,让我们以一种比我通过短推文或简短电子邮件更完整的方式解决它。
SHA-1 非常适合 k-匿名
让我们从 SHA-1 提出的实际问题开始。实际上,存在多个问题,第一个是在在线系统中存储用户密码的速度太快了。十多年前,我写了一篇关于我们的密码散列如何没有衣服的文章,并在那篇文章中展示了消费级硬件可以计算这些散列并因此“破解”密码的巨大速度。从那时起,摩尔定律多次使 SHA-1(或 SHA-256 或 SHA-512)的命题比以前更糟。有关如何存储密码的现代参考,请查看OWASP 的密码存储备忘单。
另一个问题与如何使用 SHA-1 进行完整性检查有关。由于算法的确定性,散列算法提供了一种比较两个文件并确定它们的内容是否相同的有效方法(相同的输入总是产生相同的输出)。如果一个可信赖的来源说“文件的散列是 3713..42”(以缩写形式显示),那么任何具有相同散列的文件都被认为与可信赖来源所描述的文件相同。正是为了这个目的,我们到处使用哈希;例如,如果我想从我的 MSDN 订阅中下载 Windows 11 商业版,我可以参考微软在下载页面上提供的哈希:

下载后,我可以使用PowerShell 的 Get-FileHash等实用程序来验证我下载的文件确实与上面列出的文件相同。 (关于你如何信任上面的哈希,我们可以讨论另一个兔子洞,但我会把它留到另一篇文章中。)
在网站上实现子资源完整性 (SRI)时,我们还使用哈希来确保外部依赖项未被修改。例如,每次这个博客从 Cloudflare 的 CDN 加载 Font Awesome 时,都会根据脚本标签的完整性属性中的哈希值进行验证(自己查看源代码)。
最后(尽管并非详尽无遗——我们在技术领域还有很多其他地方使用散列算法),我们在数字证书签名上使用散列算法。再举一个这个博客的例子,Cloudflare 颁发的证书使用 SHA-256 作为签名哈希算法:
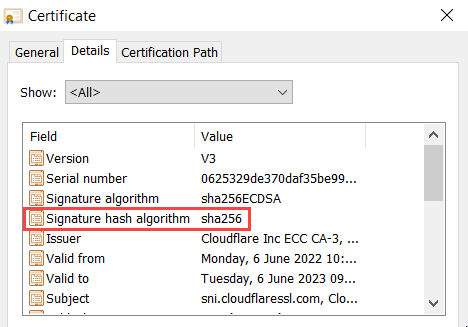
但是考虑一下:如果散列算法总是产生固定长度的输出(在 SHA-1 的情况下,它是 40 个十六进制字节),那么世界上的散列数量是有限的。在那个 SHA-1 示例中,有限数是 16^40,因为它们有 16 个可能的值(0-9 和 af)和 40 个位置。但是世界上有多少种不同的输入字符串呢?无穷!因此,必须有多个输入字符串产生相同的输出,这就是我们所说的“哈希冲突”。这有可能自然发生,尽管仅仅由于 16^40 存在大量可能性,这极不可能。但是,如果您可以制造散列冲突怎么办?我的意思是,如果您可以为现有文档获取现有散列并说“我要创建自己的文档,但是当通过 SHA-1 传递时,会产生相同的散列! ”?
五年前的现在,谷歌研究人员通过他们的SHAttered 攻击证明了这一点。他们简单的信息图讲述了这个故事:

这就是 SHA-1 完整性问题的核心:它已经不再是我们可以信赖的算法了。这就是为什么这个博客上的 TLS 证书的签名哈希算法使用 SHA-256 来代替,其中我们避开较弱算法以支持更强变体的其他示例。
所以,既然您了解了 SHA-1 的问题,让我们看看它是如何在 HIBP 中使用的,以及为什么它在那里没有问题。实际上有两个原因,我将从 Pwned Passwords 中使用的密码示例开始:
P@ssw0rd abc123 635,[email protected],+61430978216,37 example street money qwerty
那条中间线不是密码,而是解析问题。不一定是我的解析问题,事实证明你不能总是相信黑客会以干净的格式转储被破坏的数据?♂️ 所以,我没有以纯文本格式向人们提供密码,而是将它们作为 SHA-1 哈希值提供:
21BD12DC183F740EE76F27B78EB39C8AD972A757 6367C48DD193D56EA7B0BAAD25B19455E529F5EE A4DDCDA001E137C72FF8259F36BC67C5F9E083AA C95259DE1FD719814DAEF8F1DC4BD64F9D885FF0 B1B3773A05C0ED0176787A4F1574FF0075F7521E
其中 4 个哈希值很容易被破解(谷歌很擅长,只要尝试搜索第一个)就可以了;任何人都不会因为得知某个身份不明的人使用了一个通用密码而处于危险之中。不会产生任何搜索结果的 1 哈希(直到谷歌索引这篇博文……)是中间的。 SHA-1 计算速度很快,并且已经证明了针对其完整性的哈希冲突攻击这一事实并没有削弱它在保护解析错误的数据方面的作用。
第二个原因最好通过查看 API 的查询过程来解释。让我们以某人使用以下密码注册网站为例:
P@ssw0rd
这将通过许多密码复杂性标准(大写、小写、数字、非字母数字字符、8 个字符长),但显然很糟糕。因为他们正在注册一个负责在注册时检查 Pwned 密码的网站,所以该网站现在创建所提供密码的 SHA-1 哈希:
21BD12DC183F740EE76F27B78EB39C8AD972A757
让我们在这里暂停一下:无论是密码的哈希值还是电子邮件地址的哈希值,我们看到的是原始数据的假名表示。这里没有实现实质的匿名性,因为在上述特定情况下,您可以简单地通过 Google 搜索哈希,对于电子邮件地址,您几乎可以确定(除了哈希冲突),如果给定的纯文本电子邮件地址是一种用于生成哈希。
然而,这是一个不同的故事:
21BD1
这只是哈希的前 5 个字节,它被传递给 Pwned Passwords API,如下所示:
https://api.pwnedpasswords.com/range/21BD1
您可以自己轻松地运行它并查看结果,但总而言之,API 然后以 788 行响应,包括以下 5 行:
2D6980B9098804E7A83DC5831BFBAF3927F:1 2D8D1B3FAACCA6A3C6A91617B2FA32E2F57:1 2DC183F740EE76F27B78EB39C8AD972A757:83129 2DE4C0087846D223DBBCCF071614590F300:3 2DEA2B1D02714099E4B7A874B4364D518F6:1
我们在这里看到的是每个散列的散列后缀,以 21BD1 开头,后跟密码被看到的次数。事实证明,“P@ssw0rd”不是一个很好的选择,因为它是中间的那个,已经被看到了超过 83k 次。 Pwned Passwords 服务的使用者知道它是这个,因为当与前缀结合时,它与密码的完整哈希完美匹配。稍后我将详细介绍它的数学特性,现在我想解释使用 SHA-1 的第二个原因:
SHA-1 使得将整个哈希语料库分割成大致相等大小的块变得非常容易,这些块可以通过前缀进行查询。正如我已经提到的,有 16^5 种不同的可能哈希前缀,具体来说是 1,048,576 或“大约一百万”。并非每个哈希前缀都有 788 个相关的后缀,有些有更多,有些则更少,但如果我们将其作为平均值,这就解释了服务中大约 850M 的密码如何被分成一百万个较小的集合。
为什么是前 5 个字节?因为如果是前 4 个,那么每个响应都会大 16 倍,并且会开始影响响应时间。如果是前 6 个,那么每个响应都会小16 倍,并且会开始损害匿名性。 5个字符是两者之间的甜蜜点。
为什么不是 SHA-256?每个散列不是 40 个字节,而是 64 个字节,虽然我可以通过仍然只使用散列的前 5 个字符来实现相同的匿名属性,但响应中的每个后缀将是一个额外的 24 个字节并将其乘以 788 倍即使在传输层上压缩时,每个响应也要多 kb。它也是一种较慢的散列算法;仍然完全不适合将用户密码存储在在线系统中,但如果进行大量计算,它可能会对消费服务产生影响。为了什么?完整性并不重要,因为修改源密码以伪造冲突哈希没有任何价值。您会进一步将匿名性增加 16^24 的可能性,但是为什么不使用 128 字节的 SHA-512,因此比 SHA-256 还要多 16^64 的可能性?因为,正如您将在下一节中读到的,即使是 SHA-1 也提供了比您所需要的更实用的匿名性。
总之,考虑选择 SHA-1 只是为了混淆解析不佳的输入数据以保护无意中包含的信息,并将数据集合划分为易于分割和查询的集合。如果您的立场是“SHA-1 已损坏”,那么您根本不了解它的目的。
PII 和 k-匿名提供的保护
让我们将讨论更多地转向我之前提到的电子邮件地址搜索的隐私方面。原理与密码搜索相同,但在技术实现上有一个区别:查询是在SHA-1 哈希的前 6 个字节上完成的,而不是前 5 个。原因很简单:系统比密码,总共约50亿。通过 SHA-1 哈希的前 6 个字节进行查询意味着比密码搜索多 16 种可能性,因此是 16^6 或刚刚超过 16M。让我们使用这个电子邮件地址:
[email protected]
使用 SHA-1 哈希到这个值:
567159D622FFBB50B11B0EFD307BE358624A26EE
与密码搜索类似,它只是在执行查询时发送给 HIBP 的前缀:
567159
那么,戴上隐私帽,当服务将这些数据发送到 HIBP 时会有什么风险?从数学上讲,在接下来的 34 个字符未知的情况下,这个前缀可能属于 16^34 个不同的可能散列。只是为了真正做到这一点,给定一个 6 字节的 SHA-1 哈希前缀,您可以在 87,112,285,931,760,200,000,000,000,000,000,000,000,000 中取 1 来猜测完整的哈希前缀是什么。然后由于无限数量的潜在输入字符串,将该数字乘以……嗯……无穷大。这是它可以代表的可能电子邮件地址的总数。根据该术语的任何定义,前 6 个字节绝对不会告诉您正在搜索的电子邮件地址是否有用。
但是我们留下了一个更语义化的,可能是哲学性的问题:“567159”是个人身份信息吗?实际上,不,出于所有意图和目的,如果没有剩余的 34 个字符,就不可能分辨出这属于谁,即使那样,您仍然需要能够破解该哈希值,这很可能只有在您有字典时才会发生电子邮件地址的工作通过其中给定的一个出现。但它源自假名 PII,这就是偶尔 [插入填写文书工作但在这里没有技术理解的人的头衔] 失去理智的地方。
用更通俗的术语来解释这一点,就像说我上面使用的电子邮件地址开头的“t”是个人识别。真的吗?我自己的电子邮件地址以“t”开头,所以它一定是我的!这是一个无稽之谈。
我将总结一个定义,我喜欢NIST 是最好的,不仅因为它清晰简洁,而且因为它们是这类事情的重要权威来源(实际上是他们关于禁止以前违规语料库中的密码的指导)引导我首先创建 Pwned 密码):
允许通过直接或间接方式合理推断信息适用的个人身份的任何信息表示。
电话号码是 PII。物理地址是 PII。 IP 地址是 PII。某人电子邮件地址的 SHA-1 哈希的前 6 个字节不是PII。
概括
我上面解释的所有误解都没有影响这些服务的采用。 Pwned Passwords 现在每月执行超过 20亿次查询,并且直接从 FBI 持续提供新密码。对电子邮件地址的 k 匿名搜索每月会看到超过 1 亿次查询,并且被纳入从浏览器到密码管理器再到身份盗用服务的所有内容中。这些服务的成功不是由于我的任何技术天才(再次向 Cloudflare 致敬),而是由于它们简单而有效的实现(几乎)每个人都可以轻松理解?
原文: https://www.troyhunt.com/understanding-have-i-been-pwneds-use-of-sha-1-and-k-anonymity/