最近的两篇文章是关于曼德布洛特集的,它是复数集c ,迭代次数为
f ( z )= z² + c
保持有界。很容易看出,如果在任何一步 | z | > 2,迭代序列将趋于无穷大。
对于每个c ,我们可以查看逃逸时间,即值的大小大于 2 之前所需的迭代次数。曼德布洛特集是逃逸时间无限的点集。
在下面的图中,我随机采样了 1,000,000 个点,并根据相应的逃逸时间对每个点进行了着色。较浅的蓝色代表较早的逃逸时间。
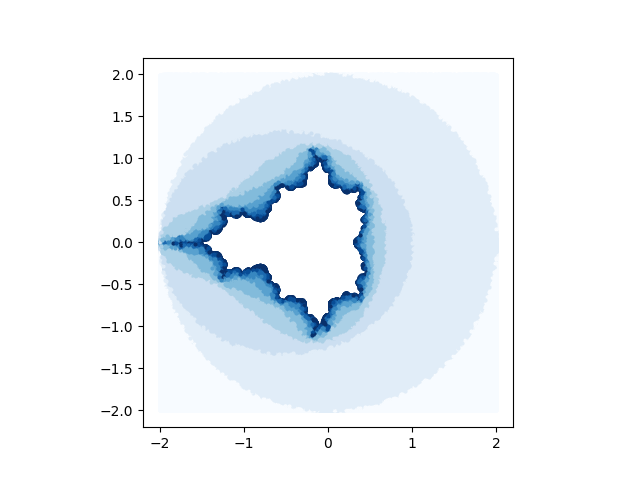
内部的白点的逃逸时间大于 10(也可能是无穷大)。
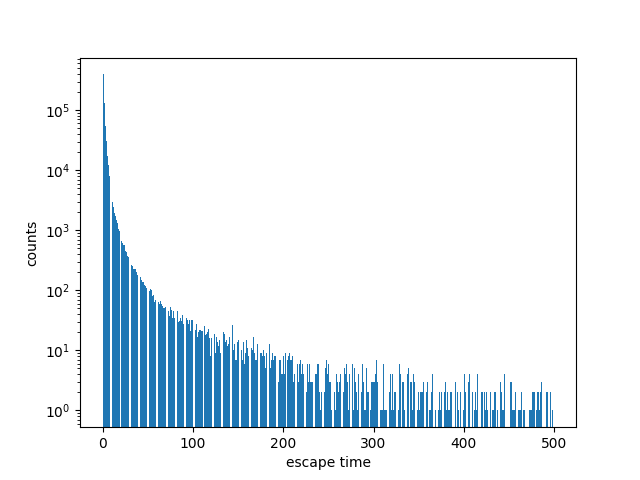
在绘制曼德布洛特集时,如何知道一个点是否永远不会逃逸?你无法确定。但通过观察逃逸时间的分布,你会发现大多数即将逃逸的点都会很快逃逸。例如,在对 1,000,000 个点进行采样后,对每个点进行 2000 次迭代,99.9% 的逃逸点会在 248 次迭代内完成。
如果我们绘制逃逸时间的直方图,它看起来就像左端的一个尖峰。使用对数刻度作为纵轴可以让我们更清楚地看到正在发生的事情。请注意,即使在对数刻度下,逃逸时间也会迅速下降。
通过计算未逃逸的点的比例,我们可以计算出曼德布洛特集面积的蒙特卡洛估计值,事实上这是计算面积的最佳方法。面积可以用无穷和来精确表示,但和的收敛速度太慢,无法使用;而蒙特卡洛采样速度更快。
使用 1,000,000 个随机c值,在 2,000 次迭代内,正方形 [-2, 2] × [-2, 2] 中总共有 905,444 个点逃逸。由于正方形的面积为 16,因此我们估算
A = 16 × (1000000 − 905,444)/1000000 = 1.5129。
该区域的 95% 置信区间为
A ± 16 × 1.96 × ( p (1 − p )/1000000)= (1.5082, 1.5176)
其中p = 905444/1000000。
一项研究 [1] 发现该面积为 1.506484 ± 0.000004,刚好超出我们的置信区间。这种差异部分是由于偶然因素造成的,部分是由于我们在 2000 次迭代时停止了。如果我们进行更多次迭代,就会有更多点逃逸(尽管数量不会很多,原因如上所述)。
[1] 参见 OEIS A098403
曼德布洛特区域和逃逸时间一文首先出现在John D. Cook上。
原文: https://www.johndcook.com/blog/2025/09/08/mandelbrot-area-and-escape-times/