极简曼德布洛特集 – 搞英语 → 看世界

曼德布洛特集是最著名的分形之一。它由复数c组成，并且迭代

f （ z ）= z² + c

是有界的。曼德布洛特集的图是一个复杂的图像——毕竟它是一个分形——然而，对曼德布洛特集的一级近似值有一个简单的描述。

如[1]所示，磁盘的图像

A = {α：|α| < ½}

在映射下，取z到z − z ² 给出f的迭代收敛于某一点的所有点的集合。

[1] 还表明

B = { c :|1+ c |<¼}

使得f ( f ( z )) 收敛于一个不动点。

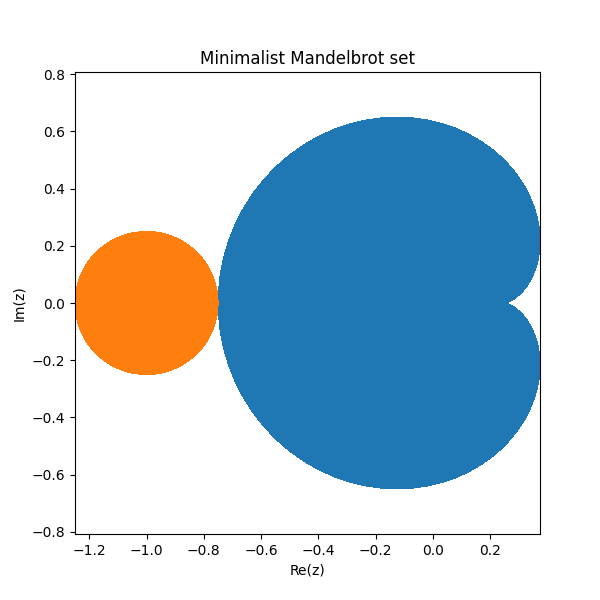
曼德布洛特极简主义.png

这两部分构成了曼德布洛特集合的核心。右边的蓝色心形区域是A ，左边的橙色圆盘是B。

曼德布洛特集合的其余部分是f的迭代保持有界但行为比A或B中的点更复杂的点。

[1] Alan F. Beardon。有理函数迭代。Springer-Verlag，1991 年。