Pick 定理的直觉 – 搞英语 → 看世界

皮克定理是一个令人惊讶且有用的定理，它可以用来计算网格上连接点所形成区域的面积。该区域的面积简单来说就是

A = i + p /2−1

其中i是内部点的数量， p是周边点的数量。

例子

例如，下图中周边有 11 个黑点，内部有 17 个蓝点。

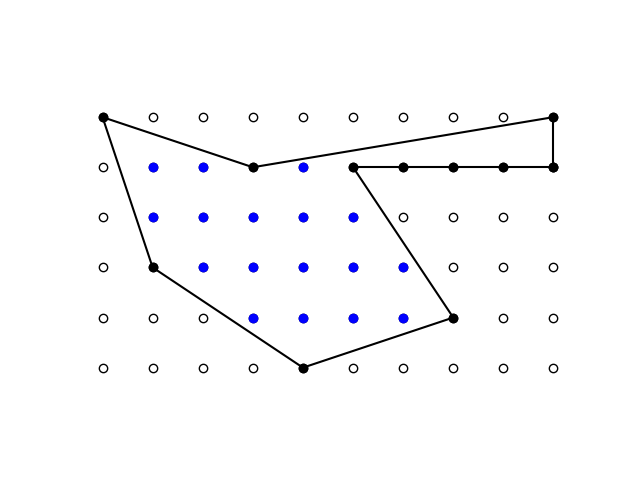
因此，皮克定理指出该图形的面积为 17 + 11/2 − 1 = 21½。

如果图形很大，面积大约为i ，这很有道理。但是，为什么需要加上周长上一半的点，又为什么要减去 1 呢？

皮克定理很简单，但并非显而易见。如果它显而易见，那么更接近笛卡尔（1596-1650）时代的人早就发现了。然而，这个定理是由乔治·亚历山大·皮克于1899年发现的。然而，对于矩形来说，这个定理相当显而易见，本文将对此进行说明。对于矩形，你可以很容易地理解为什么需要加上一半的周长点并减去1。

想象一个m x n的矩形点阵。如果在这些点阵周围画一个框，矩形的角正好位于点阵之间，那么面积就是mn ，即框内点阵的数量。

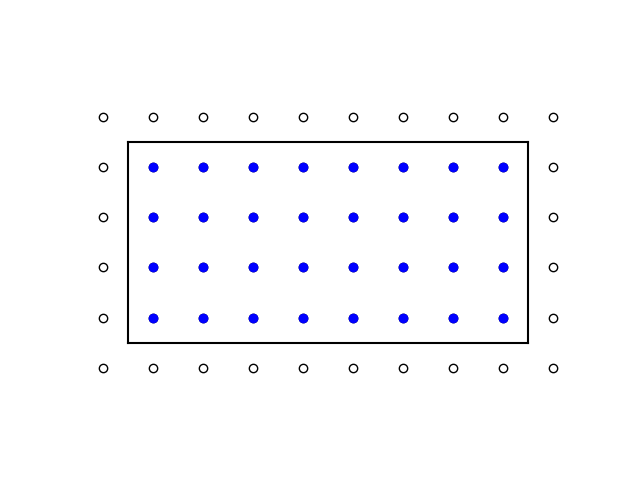
皮克定理在这里不适用，因为我们框架的角不在网格上。所以，让我们将网格向下向左移动，使其角位于网格上。

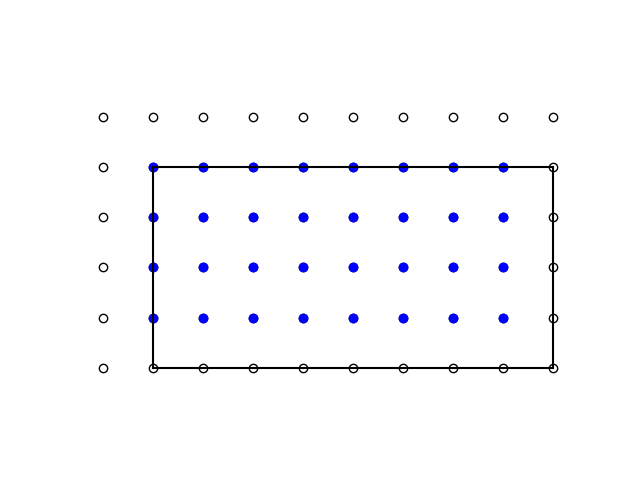
现在，我们原来的一些点（标记为蓝色）位于框架的边缘。我们可以增加边缘上的点数来修正这个问题，但这样做太多了，因为边缘上的蓝点只位于左侧和顶部。每个点在右侧和底部都有一个反射，标记为红色。所以我们不应该添加边缘上的所有点，而应该只添加边缘上一半的点。

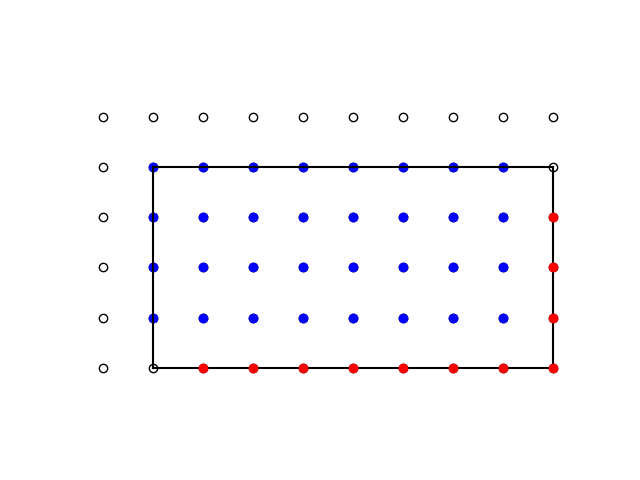
但这仍然略微多算了一点。周长上有两个点既不对应蓝点，也不对应蓝点的反射。它们是右上角和左下角的空心圆圈。所以，当我们取周长的一半时，需要减去1来计算这对点的一半。

这并不能证明皮克定理的普遍性，但它确实证明了矩形区域上的皮克定理。即使我们不明白为什么这个公式能够推广到更复杂的区域，我们也应该庆幸它确实如此。