我最近偶然读到Katherine Stange [1]写的一篇关于Lehmer的因式分解模板[2]的文章。在电子计算机出现之前,这些模板是进行中等大小数因式分解的有效方法的基础。
这篇文章将描述模板并使用 Python 脚本模拟它们的使用。
误解
当我开始阅读[1]时,我有三个误解阻碍了我对这篇文章的理解。为了避免大家也抱着同样不切实际的期望来阅读这篇文章,我先来解释一下这三个误解。
首先,当我看到一些关于用模板进行因式分解的东西时,我以为它们会像阿里托斯特尼筛法那样,模板上剪掉了 2、3、5 等的倍数。但事实并非如此;莱默的方法比这更复杂。
其次,与第一点相关,我以为因式分解法需要把模板放在一大堆数字格子上,其中包含你想要分解的数字。但事实并非如此。模板可以用来分解九位数,而一张包含超过十亿个数字的表格并不实用。
第三,我以为圆形模板上孔的位置可能具有某种几何意义。其实没有。模板设计成圆形只是为了方便。
模板的工作原理
Lehmer 制作了一套 295 个模板。Katherine Stange 在她的Github 仓库中上传了一套此类模板的 SVG 文件。下图是对应数字 42 的模板。
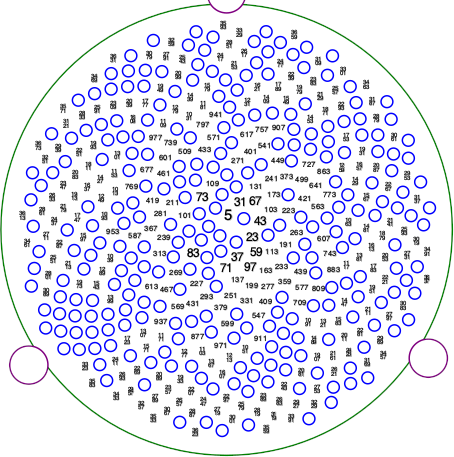
我想要关注的是模板如何工作,而不是它们为什么工作。
要分解一个数N 的因式,你首先需要找到一些与N相关的数X 1 , X 2 , X 3 , … X k ,这些数很容易手工计算。然后,你需要将与X i对应的模板叠放在一起,对着光进行计算。
如果y是模N 的二次剩余,则y也是模 N的每个素因数的二次剩余。每个模板都会将潜在素因数的数量减少大约一半。
一旦找到可能的质因数,就可以用长除法对其进行测试,然后就可以确定该数字是否是一个质因数。
每个模板是什么?
那么这些X i是什么以及其中的漏洞是什么?
X i是模N 的二次余数,即满足
X i = x ² mod N
有一个解。这可能需要一些手算,但计算量远不及独自分解N的计算量。Katherine Stange 的这个视频和这份 PDF 文档介绍了一些用于求二次剩余的算法。
注意:难点不在于求二次剩余 mod N ;你可以用对随机整数求平方 mod N来求。难点在于找到与你可用的模板集对应的二次剩余。
模板上的孔对应于 48593 以内的素数。如果X是二次剩余 mod X ,则圆盘X 上有一个素数p的孔。如果X是二次剩余 mod p和 mod N ,则p能整除N 的概率是 50%。
48593 是第 4999 个素数,因此每个磁盘上都有对应 4999 个素数的位置。莱默将这些位置排列成螺旋状,但它们也可以排列成网格或其他任何图案。
Python 模拟
请参阅上面提到的 Github 仓库,获取用于制作物理模板 SVG 文件的 Python 代码。下面的 Python 代码模拟的是模板的操作,而不是它们的几何形状。我编写这段代码是为了便于说明,而不是为了成为实用高效的整数因式分解代码。
首先,这是制作模板的代码。这里的 1 代表一个孔。
从 sympy 导入 primerange、legendre_symbol 从numpy导入数组 primes = array([p for p in primerange(3, 48594)]) 定义模板(x): # 如果 x 是二次剩余,则模板在位置 k 处有 1 # 对第 k 个奇素数取模,否则取 0 返回数组([如果 legendre_symbol(x,p)> = 0 则为 1,否则为 p 在素数中为 0])
接下来我们选择一个N和一些模N的小二次剩余。
年份 = 19972009 x = [2, 61, 79, 185, 238, 255, 313, 421, 491]
将模板相乘得到 1,其中每个模板都有一个孔。
蒙版 = 模板(x[0]) 对于范围内的 i (1,len (x)): 蒙版 *= 模板(x[i]) ps = 掩码*素数 打印(ps[ps != 0])
这将打印以下内容:
[97 103 1367 1999 15241 28351 35353 36847 44953]
然后我们测试这些素数是否都是N的因数,事实上
19972009 = 97 × 103 × 1999。
每个模板有 4999 个素数,如果 9 个模板中每个模板消除大约一半的素数,我们预计会有大约 4999/2 9 ≈ 10 个候选素数,这与我们得到的结果非常接近。
相关文章
[1] DN Lehmer 的巧妙物理因式分解装置。《数学视野》,第 30 卷第 2 期,2022 年 11 月。
[2] D.N. Lehmer 和他的儿子 D.H. Lehmer 都是数论学家。我在博客中多次提到后者,最近一次是在这里。几周前我还引用了 Katherine Stange 的观点。
分解模板一文最先出现在John D. Cook身上。
原文: https://www.johndcook.com/blog/2025/08/17/factoring-stencils/