我已经好几个月没有为Quamina开发任何新功能了,部分原因是现实生活中的种种干扰,但也因为在大规模实现正则表达式时遇到了棘手的性能问题。我仍在寻求突破,但学到了一些关于构建和执行有限自动机的知识,我认为值得分享。这篇文章与epsilon有关;任何研究过有限自动机的人都应该了解它,但我将提供一些背景知识,供那些人参考。
我之前在Epsilon Love中写过这个。一位评论者指出,那篇文章中“epsilon”的定义与标准有限自动机理论并不完全一致,但它仍然很有用,因为它描述了 epsilon 如何支持类似 shell 风格的“ * ”这样的结构。
背景
有限自动机有两种类型:确定性自动机 (DFA) 和非确定性自动机 (NFA)。DFA 每次输入一个符号,从一个状态转移到另一个状态:它简单易懂,易于实现。NFA 有两个显著特点:首先,当你处于某个状态,并且一个输入符号到达时,你可以转移到多个其他状态。其次,一个状态可以有“epsilon 转换”(我们用“ε”来表示 epsilon),它可以在你处于该状态的任何时候发生,无论是否有输入。
NFA 的遍历更加复杂(下文会讨论),但如果你想用. 、 ? 、 *等符号来实现正则表达式,就需要它们。你可以把任何 NFA 转换成 DFA,我会在以后的文章中继续讨论这个话题。
为了实现 NFA,我一直使用Thompson 构造,其中“Thompson”指的是Ken Thompson ,Unix 的共同创始人。Russ Cox 在《正则表达式匹配可以简单又快速》一文中也对这项技术进行了很好的描述。您无需学习它也能理解这篇文章,但我会用“基于 Thompson”来解释设计选择的合理性。
今天我将讨论两个具体问题,ε-闭包和更简单的 NFA 定义。
ε-闭包
为了做好准备,请考虑以下正则表达式: A?B?C?X
它应该匹配“X”、“BX”和“ACX”等等,但不匹配“CAX”或“XX”。Thompson 建议你实现A?在“A”上创建一个到下一个状态的转换,然后再创建一个到下一个状态的 ε 转换;因为如果你看到“A”,你就应该转换,但即使你没有看到,你也可以进行转换。
生成的 NFA 如下所示:
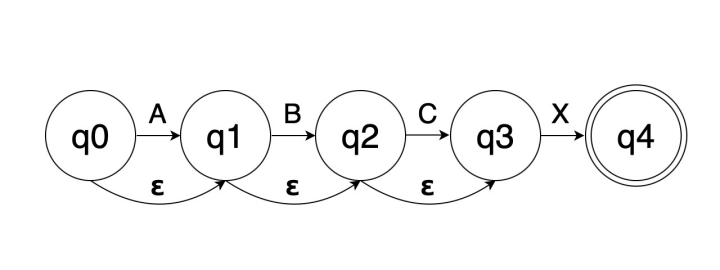
在有限自动机数学中,状态通常用字母“q”后跟一个数字来表示(通常用斜体和下标表示,例如q 0 ,但这里不是,抱歉)。注意q4的双圆,它表示这是一个目标状态,也就是说,如果我们到达这里,就匹配了正则表达式。我应该补充一下,这是用draw.io生成的,它似乎让这类事情变得简单。
回到那个NFA
所以,这里有一个挑战:在脑子里勾勒出遍历代码。思考一下输入字符串“AX”和“BCX”以及“X”,以及如何通过NFA到达Q4目标状态。
诀窍在于所谓的 ε-闭包。当你到达某个状态时,在查看下一个输入符号之前,你必须做好准备来处理它。在这种情况下,你需要能够在 A、B 或 C 上进行转换。所以你要做的是将起始状态q0以及通过 ε-转换可以到达的任何其他状态组合在一起。在这种情况下,起始状态的 ε-闭包是{q0, q1, q2, q3} 。
那么,假设你看到一个“B”输入符号。你将它应用于ε闭包中的所有状态。只有q1匹配,因此转换到q2 。在查看下一个输入符号之前,你计算q2的ε闭包,结果是{q2, q3} 。有了这个ε闭包,你可以匹配“C”或“X”。如果匹配到“C”,你将跳转到q3 ,它的ε闭包就是它本身,因为“X”是唯一的前进路径。
因此,一步的 NFA 遍历算法将变成如下形式:
-
从州列表开始。
-
计算该列表的 ε-闭包。
-
读取输入符号。
-
对于 ε 闭包中的每个状态,查看是否可以遍历到另一个状态。
-
如果是,请将其添加到您的状态输出列表中。
-
完成后,您的状态输出列表将成为该算法下一步的输入。
计算问题
假设你的正则表达式是(A+BC?)+ 。我不会画出这个 NFA 的草图,但只要看一下就能知道它必须有回环;一旦你匹配了括号中的部分,你就需要回到一个可以识别另一个出现的状态。对于这个正则表达式的 NFA,计算 ε-闭包可能会导致你陷入无限循环。(这应该是显而易见的,但我直到第一次发生之后才意识到。)
可以有循环,也可以有重复。实践中,一个状态有多个 ε 转换,并且这些转换的目标重叠的情况并不少见。
所以你需要注意循环并对输出进行重复数据删除。我认为避免这种情况的唯一方法是使用 cookie-crumbs 记录“我去过的地方”的轨迹,可以是列表或哈希表。
这两种方法都是有问题的,因为它们需要分配内存,而当您尝试以 Quamina 每秒数百万的历史速度将模式与事件进行匹配时,您真的不想这样做。
我将在未来的 Quamina-Diary 活动中深入研究这个问题,但显然,缓存计算出的 epsilon 闭包将避免重新进行此计算。
无论如何,请记住 ε-闭包,因为随着本系列的继续,它们会不断出现。
最后,简化“NFA”
在本文的开头,我给出了 NFA 的标准定义:首先,当你处于某个状态,并且一个输入符号到达时,你可以转移到多个其他状态。其次,你可以有 ε-转移。根据我最近的工作,我认为这个定义是多余的。因为如果你需要在某个输入符号上转移到两个不同的状态,你可以用 ε-转移来实现。
这是一个迷你 NFA,它从“A”上的状态q0转移到q1和q2 。
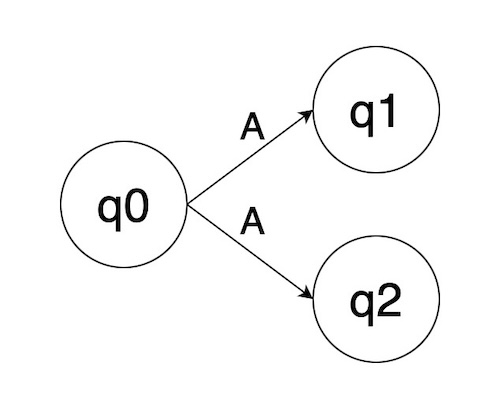
下面展示了如何使用 ε-transitions 实现相同的效果:
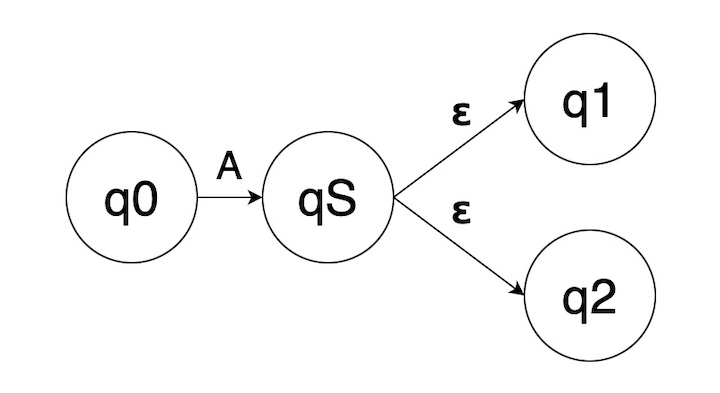
在该 NFA 中, qS中的“S”代表“拼接”,因为它是存在用于连接两个有限自动机遍历线程的状态。
我非常确定这不仅仅是一个数学上的等价关系。在我的正则表达式实现中,至少到目前为止,我从未遇到过需要进行第一种双重转换的情况。此外,“拼接”结构正是 Thompson 实现正则表达式“ | ”运算符的方式。
因此,如果您正在构建 NFA,则在一个状态下所需的所有遍历内容都是从输入符号到下一个状态的简单映射,以及 ε-转换列表。
下一步
我自己实现的 NFA 遍历是如何与 Benchmark From Hell 发生正面冲突并且至今仍未恢复的。
原文: https://www.tbray.org/ongoing/When/202x/2025/07/07/Epsilon-Wrangling