园丁椭圆 – 搞英语 → 看世界

定义椭圆有几种方法。如果你想用软件绘制椭圆，最方便的方法是使用参数化的形式：

$\begin{align*} x(t) &= h + a \cos(\theta) \cos(t) - b \sin(\theta) \sin(t) \\ y(t) &= k + a \sin(\theta) \cos(t) + b \cos(\theta) \sin(t) \end{align*}$

这给出了一个以 ( h , k ) 为中心的椭圆，其长半轴为a ，短半轴为b ，长轴相对于水平方向旋转了 θ 角。

但如果要实际画椭圆，有一个更方便的定义：椭圆是到两个焦点的距离之和为常数s的点集。这种方法通常被称为园丁椭圆。它也被称为钉子和绳子法，后者更具描述性。

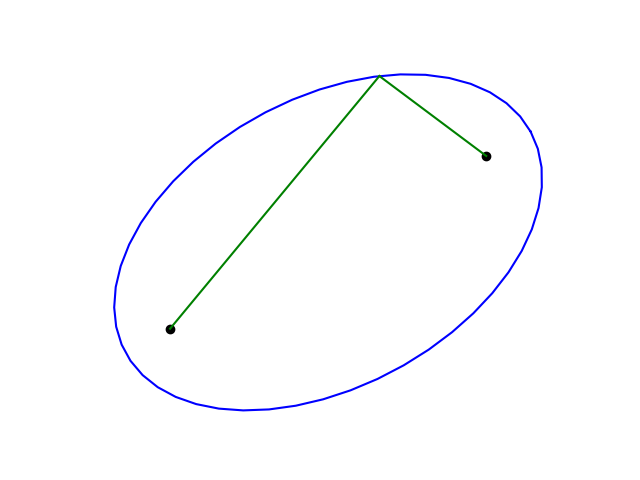
园丁1.png

要在一块胶合板上画一个椭圆，需要在胶合板的两个焦点处分别钉上一个钉子，并将一根长s的绳子的一端分别固定在每个钉子上。然后，将一支铅笔放在绳子的中间，并拉紧。移动铅笔时，绳子要保持绷紧。这样就能画出一个椭圆[1]。

据推测， “园丁椭圆”这个名字来源于更大规模的相同想法，例如园丁使用地面上的两个木桩和一些绳子划出一个椭圆形的花坛。

回到电脑屏幕上的绘图，园丁椭圆有一个实际用途：要判断一个点是否在椭圆内，只需将该点到椭圆每个焦点的距离相加即可。如果和小于s ，则该点在椭圆内。如果和大于s，则该点在椭圆外。

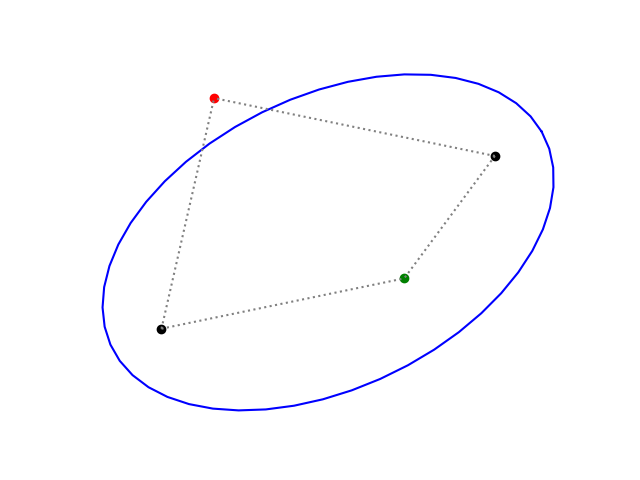
园丁2.png

从参数到钉子和绳子

如果您有椭圆的参数形式，您如何找到园丁的方法表示？

为了更容易描述点，暂时设 θ = 0 且h = k = 0。则焦点位于 (± c , 0)，其中c ² = a ² − b² 。

因为 ( a , 0) 是弦上的一个点，你必须能够画出它，所以弦必须从焦点 (− c , 0) 延伸到点 ( a , 0)，再回到焦点 ( c , 0)。因此，弦的长度为2a 。

弦的长度取决于长轴，而不是短轴。

当我们移动和旋转椭圆时，让 θ、 h和k取可能的非零值，我们对焦点应用相同的变换。

$\begin{align*} F_1 &= (h - c\cos(\theta), k - c\sin(\theta)) \\ F_2 &= (h + c\cos(\theta), k +\, c\sin(\theta)) \\ \end{align*}$

旋转和平移椭圆不会改变长轴的长度，因此s保持不变。

[1] 在实践中，木匠可能想用不同的方式画一个椭圆。

园丁椭圆最初出现在John D. Cook 的文章中。

原文： https://www.johndcook.com/blog/2025/06/01/gardeners-ellipse/

从参数到钉子和绳子

相关文章