将抛物线拟合到椭圆，反之亦然

上一篇文章讨论了如何用椭圆和抛物线拟合相同的数据。两者都拟合得很好，但椭圆拟合得更好一些。这种情况经常发生，因为椭圆比抛物线多了一个自由度。

有一种方法可以将抛物线拟合到椭圆的极点：匹配端点和曲率。这会用尽抛物线的所有自由度。

当你用类似的方法将椭圆拟合到抛物线时，你会剩下一个自由度。曲率取决于一个比率，因此你可以在保持该比率不变的情况下调整参数。你可以利用这个自由度在一定区间内更好地拟合抛物线，同时仍然保持顶点的曲率一致。

该帖子的其余部分将阐明上面概述的想法。

将抛物线拟合到椭圆

假设你有一个椭圆，其方程为

（ x / a ）² + （ y / b ）² = 1。

(± a , 0) 处的曲率等于a / b ²，(0, ± b ) 处的曲率等于b / a ²。

现在如果你有一条抛物线

x = cy² + d

那么它在y = 0 处的曲率就是 2| c |。

如果要使抛物线与椭圆在（ a ，0）处匹配，则d = a 。

为了匹配 ( a , 0) 处的曲率，我们设a / b² = 2| c| 。因此c = − a /2 b² 。（如果没有负号，曲率会匹配，但抛物线会偏离椭圆。）

类似地，在 (− a , 0) 处，有d = − a且c = a /2 b ²。在 (0, ± b ) 处，有d = ± b且c = ∓ b /2 a ²。

这是一个黄金椭圆的示例。

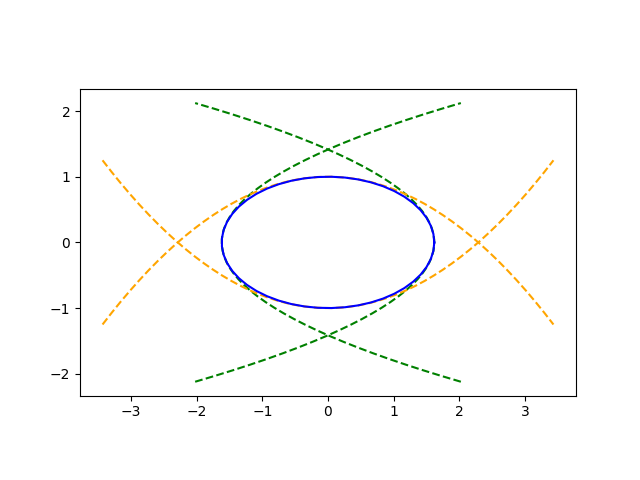
抛物线椭圆1.png

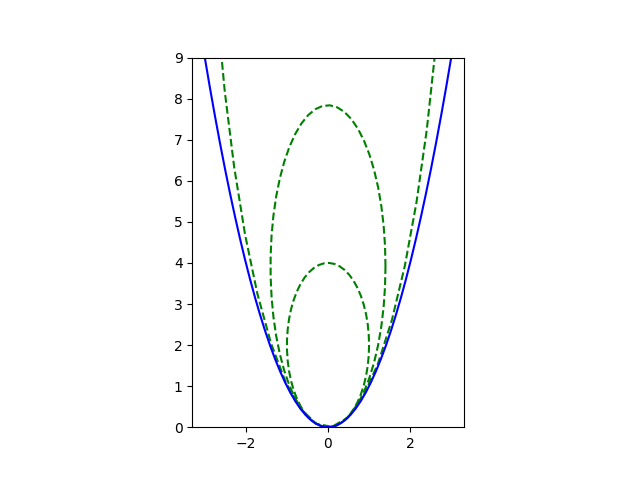
现在我们固定抛物线，比如说

y = cx²

找到一个椭圆

( x / a )² + (( y − y ₀ )/ b )² = 1

拟合顶点 (0, 0)。为了使椭圆与抛物线在顶点相切，我们必须

((0 − y ₀ )/ b )² = 1

因此y ₀ = b 。为了匹配曲率，我们有

b / 2 a² = c 。

因此， a和b并非唯一确定，只有b / a²的比值。只要该比值保持在 2c 不变，每个椭圆都会在顶点相切，并在那里曲率一致。但是，参数值越大，在更大范围内越接近抛物线。在极限情况下，当b → ∞ （保持b / a² = 2c ）时，椭圆变为抛物线。

抛物线椭圆2.png