《龙与地下城》 – 搞英语 → 看世界

Dan Piponi 在Mastodon上发布了如下图表。

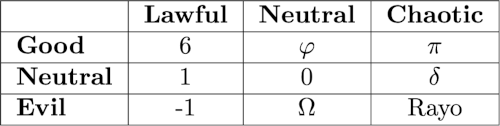
| |合法 |中性|混乱| |---------+--------+---------+---------| |好 | 6 | φ | π| |中性| 1 | 0 | δ| |邪恶| -1 | Ω|雷约 |

尽管解释起来可能会让笑话不再好笑，但我还是想解释一下丹的桌子。

上面的对齐矩阵来自《龙与地下城》，并且已经成为一种模因。

中性好数φ是黄金分割率，(1+√5)/2=1.6180339…。

想必这篇博客的读者都听说过π。它之所以出现在混沌列中，或许是因为它被认为是（但尚未被证实）一个“正态数”，也就是说，无论以何种进制表示，其数字的分布都符合正态分布。

上面的数字δ = 4.6692016……是费根鲍姆常数，我三周前提到过。我想把它放在混沌这一栏里是一种双关语，因为这个数字在混沌理论中出现过。人们认为δ是超越数，但甚至没有证据表明它是无理数。

Ω 是柴廷常数。在某种意义上，这个数字是随机生成的程序停止的概率。它是一个正常数，但也是不可计算的。计算 Ω 前n位的最小程序长度必定为O ( n )，因此任何固定长度的程序都无法生成 Ω 的位。

拉约的数字真是邪恶。据说它是最大的已知数字。定义如下：

大于任何一阶集合论语言中表达式命名的有限数的最小数，该语言仅使用 googol 或更少的符号。

你可以通过将 googol (= 10 ¹⁰⁰ ) 替换为整数n来参数化 Rayo 的定义。序列 Rayo( n ) 一开始就足够小。根据OEIS， Rayo(30) = 2，因为

30 个符号的公式“(∃x_1(x_1∈x_0)∧(¬∃x_1(∃x_2((x_2∈x_1∧x_1∈x_0)))))”唯一地定义了数字 1，而更小的公式只能定义数字 0，最小的是 10 个符号的公式“(¬∃x_1(x_1∈x_0))”。

OEIS 没有给出当n > 30 时 Rayo( n ) 的值，大概是因为即使是计算 Rayo(31) 也非常困难。