威尔金森多项式

如果稍微改变一下多项式的系数，它的零点位置会不会也随之改变？换句话说，多项式的根是否连续地依赖于它的系数？

你会这么想，而且你是对的。某种程度上来说。

很容易看出，系数的微小变化可能会导致质的变化，例如，一个重根分裂成两个彼此接近的不同根，或者一个实根获得了一个较小的虚部。但也有可能，系数的微小变化也会导致根发生相当大的移动。

威尔金森多项式就是一个著名的例子，它清楚地说明了这一点。

定义

w （ x ）=（ x -1）（ x -2）（ x -3）…（ x -20）= x – ^20-210x – ¹⁹ +…

和

W （ x ）= w （ x ） ⁻²⁻²³ x ¹⁹

因此两个多项式的区别在于前者中x ¹⁹的系数为 −210，而后者中 x 19 的系数为 −210.0000001192。

w ( x ) 和W ( x ) 的根当然很接近。但事实并非如此！

w的根显然是 1, 2, 3, …, 20。但W的根却截然不同。或者至少有些根截然不同。大约一半的根没有太大变化，但另一半根变化很大。如果我们按实部排序，16 次方根会分成两个根，分别为 16.7308 ± 2.81263 i 。

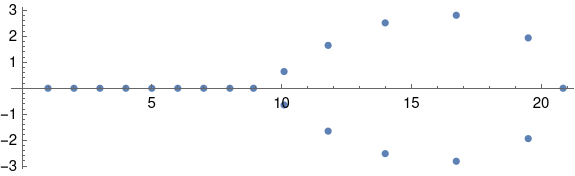
威尔金森1.png

这是生成上述图表的 Mathematica 代码。

 w[x_] := 乘积[(x - i), {i, 1, 20}]     W[x_] := w[x] - 2^-23 x^19     根 = NSolve[W[x] == 0, x]     ComplexListPlot[x /. 根]

一个系数的微小变化，就会导致根的变化高达七个数量级。威尔金森称这一发现“令人震惊”。

连续模量

多项式的零点确实连续依赖于参数，但连续模量可能非常大。

给定零点允许移动的容差ε，可以指定系数的相应精度δ来满足该容差，但为了使根具有中等精度，系数可能必须具有极高的精度。连续模本质上是ε/δ的比值，这个比值可能非常大。在上面的例子中，它大约是8,400,000。

按照δ-ε连续性的定义，每个ε都有一个δ。但这个δ可能必须比ε小几个数量级。

连续模是一个重要的概念。在实际应用中，如果连续模很大，函数是否连续可能并不重要。在这种情况下，函数在实际应用中可能是不连续的。

连续性是一个离散概念——一个函数要么连续，要么不连续——但连续模是一个连续概念，这种区别可以解决一些明显的悖论。

例如，考虑区间 [0, 1] 上的函数序列f _n ( x ) = x ⁿ 。对于每个n ， f _n都是连续的，但极限不是连续函数：当x < 1 时，极限等于 0，当x = 1 时，极限等于 1。

但这从连续模的角度来说说得通。f n ( x )_的连续模为n 。因此，虽然该序列在n较大时是连续的，但随着连续模的增加，它变得“不那么连续”。