欧几里德算法的运行时间分布 – 搞英语 → 看世界

当您为算法提供一对连续的斐波那契数时，欧几里德算法的最坏情况运行时间就会发生。该算法需要n步来计算F _{n +1}和F _{n +2}的最大公约数。

第 n个斐波那契数是最接近 φ ⁿ /√5 的整数，其中 φ = (1 + √5)/2 是黄金比例。您可以取对数并求解最大的n ，使得F _n小于x ，减去 2 ，并确定找到小于x的两个数字的 gcd 所需步骤数的上限。

但是平均运行时间或运行时间的分布又如何呢？

对于较大的x ，使用欧几里德算法计算两个数字 0 < a < b < x的 gcd 所需的步数分布近似正态分布

12 log(2) log( b ) / π²。

例如，参见[1]。

让我们通过模拟来说明这一点。下面的 Python 代码返回计算 gcd( a , b ) 时使用的步数。

 def 欧几里德(a, b):         步骤 = 0         而a！= 0：             a、b = b%a、a             步骤 += 1         返回步骤 # gcd = b

我生成了 10,000 对小于 2 ⁶³的随机整数（因为最大有符号 64 位整数为 2 ⁶³ − 1），并绘制了运行时间的直方图。

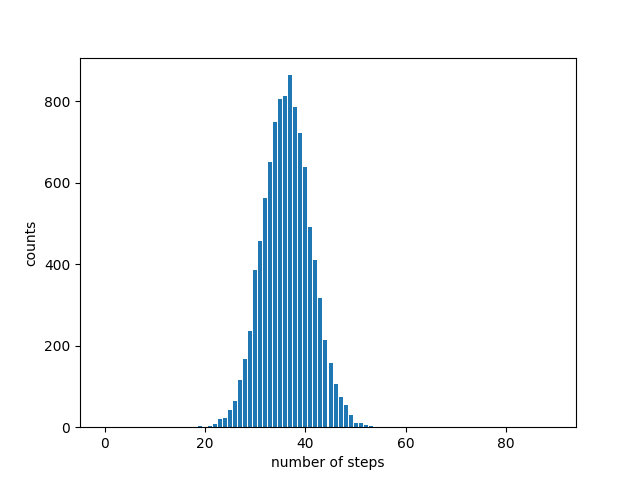
我得到了一条漂亮的钟形曲线，平均值为 36.3736。理论平均值为 0.8428 log(2 ⁶³ ) = 36.8021。

[1] 道格·汉斯利。欧几里得算法的步骤数。数论杂志 49。142–182 (1994)。