考虑在直径为 D 的圆盘上生成 N 个点的问题。该函数必须是确定性的,并且这些点在圆盘上均匀分布。重要的是,对于 N 的任何整数值,我想生成恰好N 个点。
这就是我对 $N = 1721$ 的意思:

我最近需要解决这个问题,这就是我想到的。
首先,我们知道第一个点将在原点(0,0)处进行硬编码,因此可以安全地忽略它,因为无论如何我们都会手动添加它,并且只考虑下一部分的 N-1 个点。
让我们定义一个整数 M。我们将把剩余的 N-1 个点分布在 M 个同心环上。令 $S_i$ 为环 $i$ 上的点数。我们想要:
$$ \sum S_i = N – 1 $$ 环与环之间的点数应如何变化?好吧,如果环与中心呈线性间隔,则它们的半径呈线性级数,因此让每个环的点数与环周长成正比似乎是个好主意。我们将该比例称为 $\alpha$:
$$ S_i = 2 \pi R_i \alpha $$ 我们选择均匀同心环,又名 $R_i = [1, 2, \ldots, M]$,所以:
$$ 2 \pi \alpha \sum R_i = N – 1 \ $$ 我们知道 $\sum R_i = \frac{M(M+1)}{2}$,所以: $$ \alpha = \frac{ N-1}{\pi M (M+1)} $$ 这为 $\alpha$ 提供了一个很好的值,但仍然存在为 M 选择值的问题。
让我们看看 $M$ 可能有哪些值。使用我们希望 $\alpha > 1$ 的合理约束,这给出了选择 $M$ 的二次不等式:
$$ \pi M^2 + \pi M + (1-N) < 0 $$ 当 $M$ 位于其根之间时,该二次多项式将为负数。由于我们显然想要正数的环,这给了我们 $M$ 的界限。让我们看看该多项式对于 1 到 20 之间的整数值的根:
N M1 M2 1 0.25 -1.25 2 0.44 -1.44 3 0.60 -1.60 4 0.73 -1.73 5 0.86 -1.86 6 0.97 -1.97 7 1.07 -2.07 8 1.17 -2.17 9 1.26 -2.26 10 1.35 -2.35 11 1.44 -2.44 12 1.52 -2.52 13 1.59 -2.59 14 1.67 -2.67 15 1.74 -2.74 16 1.81 -2.81 17 1.88 -2.88 18 1.95 -2.95 19 2.01 -3.01 20 2.07 -3.07不仅正根生长得很慢,而且我们必须小心舍入。在本文的其余部分中,我将选择 $M$ 的最大值,可以这么说,它给出了点的最大“密度”。但任何小于该值的值都是可能的。使用较低的 M 值可实现更“环状”的采样,使用最大值可实现最“密集”的采样。
因此,最大 M 值的公式如下:
$$ M_{max} = \text{floor} \Big( \frac{-\pi + \sqrt{\pi^2 – 4\pi(1-N)}}{2 \pi} \Big) $$现在我们有了 $M$ 和 $\alpha$,从上面的公式得到 $S_i$ 很容易!这是 N=50 时我们得到的结果:
import numpy as np N = 50 M = np.floor((-np.pi + math.sqrt(np.pi**2 - 4*np.pi*(1-N))) / (2*np.pi)) alpha = (N-1)/(math.pi*M*(M+1)) R = np.arange(1, M+1) S = 2*np.pi*alpha*R print(S) print("sum = ", S.sum())
[ 8.16666667 16.33333333 24.5 ] sum = 49.0
是的!我们明白了!这就是我们每环的点数,总和是完美的 $N-1 = 49$!加上额外的中心点,这就是我们想要的 50 个!
但是等等!这些是实数……我们需要每个环的整数个点。我们如何从 $S_i$ 转换为整数数组?
嗯,可能有很多方法可以实现这一点。对我来说,我选择一个简单的技巧。首先,对 S 进行舍入并再次检查总和。运气好的话,这个金额仍然是 $N – 1$。如果不是,则从 $S_i$ 的最后一个元素中减去差值。这是快速而简单的,最后一个环是得分最多的环,使得这个选择几乎不引人注目。
将每个环的点数转换为实际点坐标只需在极坐标中采样并转换为笛卡尔坐标即可。这是Python中完整的uniform_disk_sampling()函数:
import numpy as np def uniform_disk_sampling(N, diameter): M = np.floor((-np.pi + np.sqrt(np.pi**2 - 4*np.pi*(1-N))) / (2*np.pi)) if M == 0: M = 1 alpha = (N-1)/(np.pi*M*(M+1)) R = np.arange(1, M+1) S = 2*np.pi*alpha*R # If we're off, subtract the difference from the last element S = np.round(S) S[-1] -= (S.sum() - (N - 1)) S = S.astype(int) # List of sample points, start with the origin point points = [np.zeros((1, 2))] for s, r in zip(S, R): theta = np.linspace(-np.pi, np.pi, s+1)[:-1] radius = r/M * diameter/2 points.append(np.column_stack((radius*np.cos(theta), radius*np.sin(theta)))) return np.vstack(points)
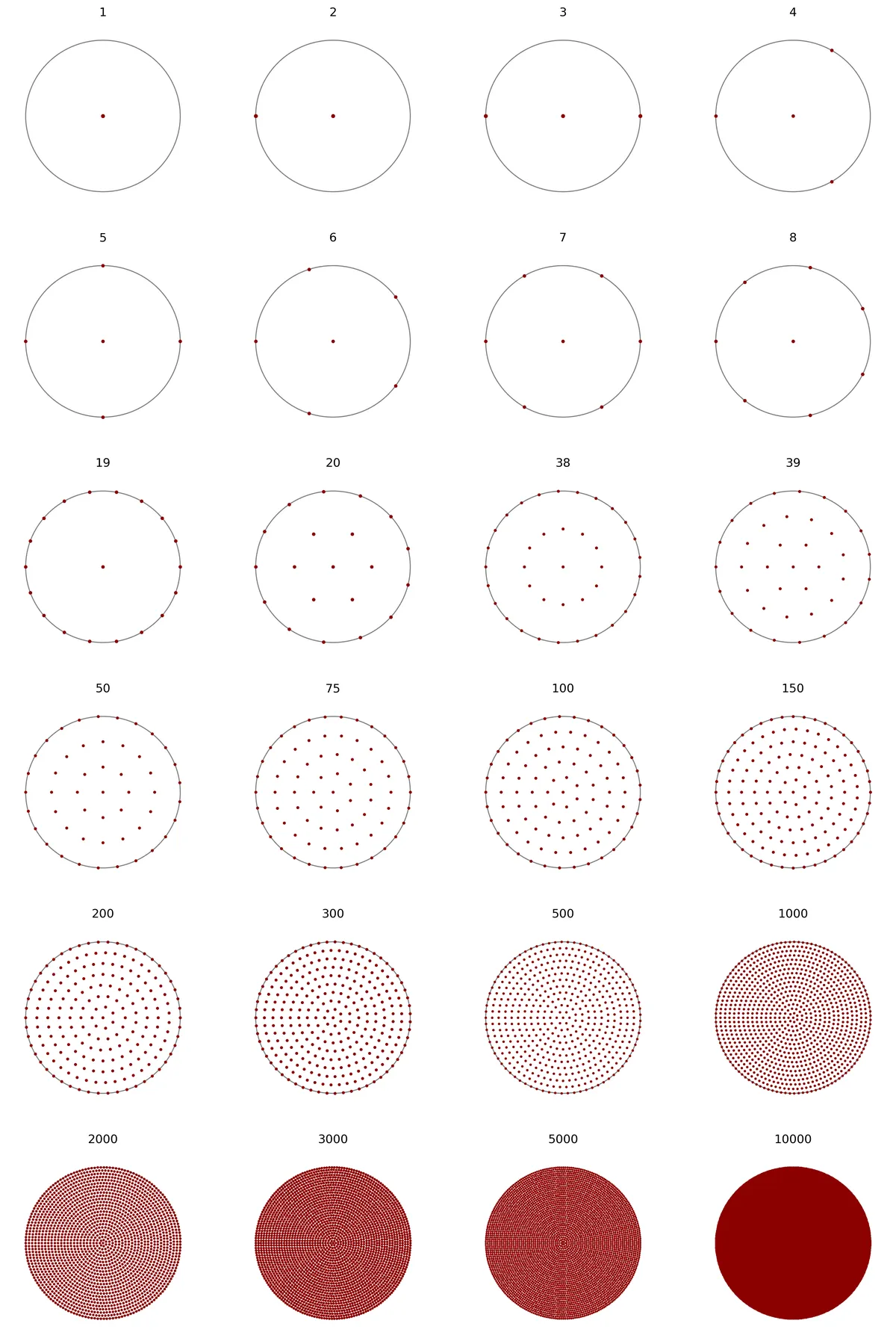
这就是从 N=1 到 10000 的样子:
原文: https://victorpoughon.fr/non-random-uniform-disk-sampling/