我最近遇到了雷卡曼的序列。 NJA Sloane,在线整数序列百科全书的创始人称雷卡曼序列是他最喜欢的序列之一。它在 OEIS 中的序列为 A005132 。
该序列从 0 开始,序列中的第n个数字是从前一个数字向前或向后移动n步的结果。如果结果为正且您尚未访问过号码,则可以向后移动。否则你就继续前进。
以下是生成序列的前N 个元素的 Python 代码。
def 雷卡曼(N): a = [0]*N 对于范围 (1, N) 中的 n: 提案 = a[n-1] - n 如果提案 > 0 并且提案不在集合(a)中: a[n] = 提案 别的: a[n] = a[n-1] + n 返回一个
例如, recaman(10)返回
[0、1、3、6、2、7、13、20、12、21]
有一个Numberphile视频对序列做了两个有趣的事情:将序列可视化并以音乐的形式播放序列的表示。
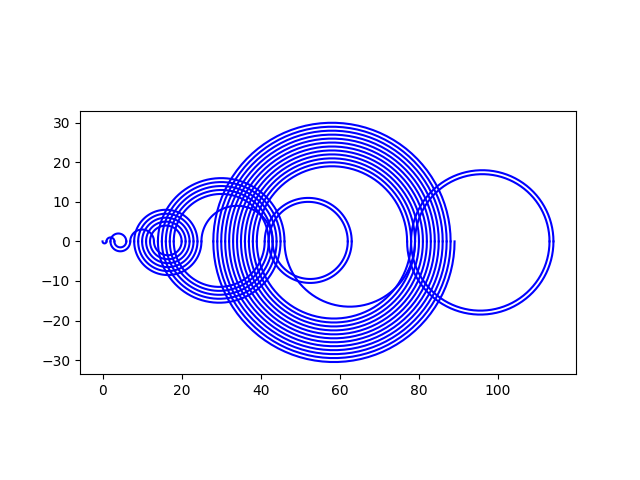
可视化的规则是用圆弧连接序列的连续元素,数轴上方和下方交替出现圆弧。
这是从视频中重现图像的代码。
将 numpy 导入为 np 将 matplotlib.pyplot 导入为 plt def draw_arc(a, b, n): c = (a + b)/2 r = 最大值(a, b) - c t = np.linspace(0, np.pi) * (-1)**(n+1) plt.plot(c + r*np.cos(t), r*np.sin(t), 'b') 数 = 62 a = 雷卡曼(N) 对于范围 (N-1) 内的 n: 绘制弧线(a[n], a[n+1], n) plt.gca().set_aspect("等于") plt.show()
这是输出:
要创建音乐序列,请将数字n与半音阶的第 n个音符相关联。您可以听视频中的音乐;这是用 Lilypond 制作的乐谱。

雷卡曼后的序列首次出现在约翰·D·库克 (John D. Cook)杂志上。
原文: https://www.johndcook.com/blog/2025/05/05/recamans-sequence/