物流地图的简单部分并不那么简单

五年前，我写了一篇博文，题为“Logisitic 分叉图” 。回顾那篇文章，它似乎并没有那么“详细”，尽管它确实比大多数流行的帐户更详细。

逻辑图由下式给出

f ( x ) = r x (1 − x )

其中x是 0 到 1 之间的变量， r是 0 到 4 之间的参数。

如果您在重复应用逻辑映射、计算f ( x )、 f ( f ( x ))、 f ( f ( f ( x )))、… 时观察x的值会发生什么情况，事情就会变得有趣：

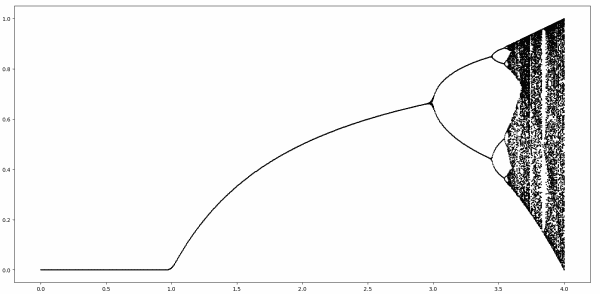
逻辑分叉图

该图显示了参数r变化时迭代的结束位置。当r ≤ 3 时，迭代收敛到单个固定点，假设严格从 0 到 1 之间开始。当r略大于 3 时，迭代在两个吸引点之间循环，然后对于较大的r ，它们在 4 个点之间反弹，然后是 8 个点，然后最终爆发混乱。字面上地。

在上图中，0 ≤ r ≤ 3 的区域似乎是简单部分。确实如此，但事情没那么简单。这篇文章将更深入地了解这部分图表中发生的情况。

四个问题

关于序列的收敛性，我们可以提出一系列问题。

我们知道，对于 0 ≤ r ≤ 3，迭代收敛到一个点。所以第一个问题的答案是肯定的。

对于 0 ≤ r ≤ 1，迭代收敛于 0。对于 0 ≤ r ≤ 3，迭代收敛于 ( r − 1)/ r 。这就回答了第二个问题。

第三、第四个问题就比较有趣了。

当 0 ≤ r < 1 时，迭代次数单调递减至 0。

当 1 ≤ r ≤ 2 时，收敛是单调的。如果x开始于固定点 ( r − 1)/ r以下，则收敛是单调递增的。如果x从上面开始，则序列是单调递减的。

当 2 < r ≤ 3 时，收敛不是单调的；一旦足够接近固定点，迭代就会交替地超出和低于固定点。这是因为f在固定点处的导数为负。

这是一个蜘蛛网图，显示r = 2.9 时的收敛不是单调的。

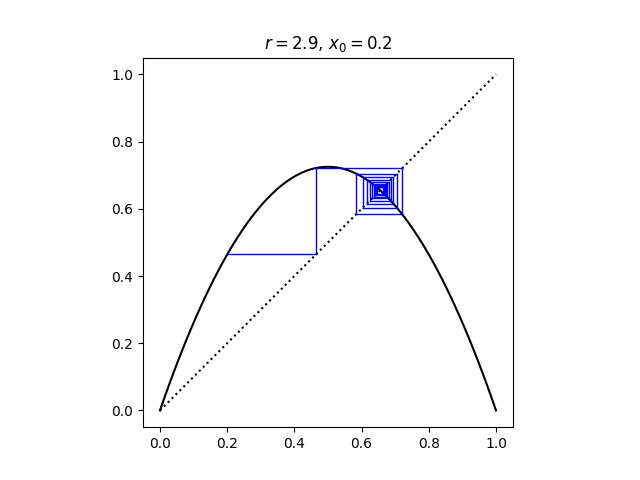
在蜘蛛网图中，单调收敛看起来像楼梯，而振荡收敛看起来像螺旋。

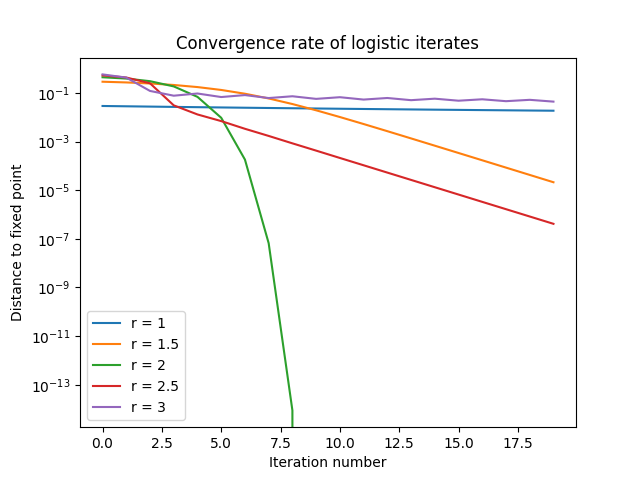
在 0 < r < 1 区域中，收敛类似于r ⁿ 。

在区域 1 < r < 2 中，收敛性类似于 (2 − r ) ⁿ 。

在 2 < r < 3 区域中，收敛也类似于 (2 − r ) ⁿ ，现在符号交替。

特殊情况是r = 1、2 和 3。 r = 1 和 3 时收敛非常慢，而r = 2 时收敛非常快。

当r = 2 时，每一步到固定点的距离都是平方的，因此收敛性是二次的。