正如上一篇文章所述,曼德布洛特集合的大部分区域来自两个区域。最大的是下方蓝色的心形区域,其次是橙色圆盘区域。
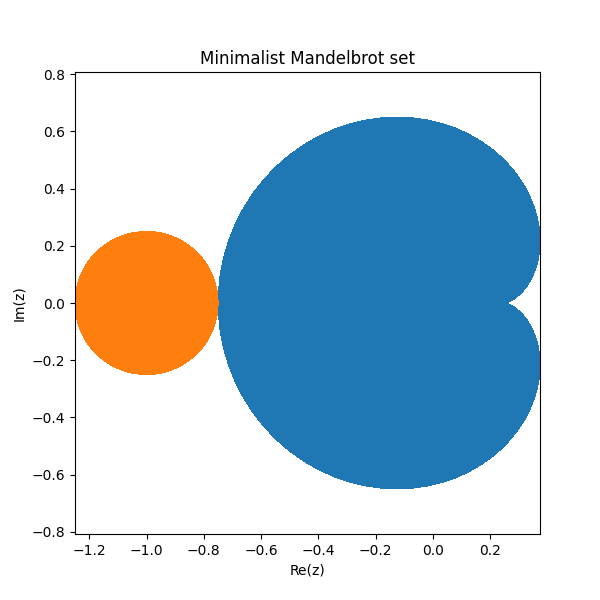
蓝色心形线表示点c的集合,使得z² + c的迭代收敛于一个不动点。橙色圆盘表示收敛于周期为 2 的循环的点集。
我们可以选择一个点,并使用以下 Python 函数在迭代之间画一条线来观察收敛情况。
导入 matplotlib.pyplot 作为 plt def plot_iterates(c): f = lambda z: z**2 + c z = c s = [z] 对于范围内的 i (1, 20): z = f(z) s.附加(z) plt.plot([s[i-1].real, s[i].real], [s[i-1].imag, s[i].imag], color="C0") plt.gca().set_aspect("平等") plt.显示()
首先,我们从心形线上的一个点开始,该点收敛到一个固定点。我们可以说它收敛到一个周期为 1 的循环。
绘图迭代(0.05 + 0.3j)
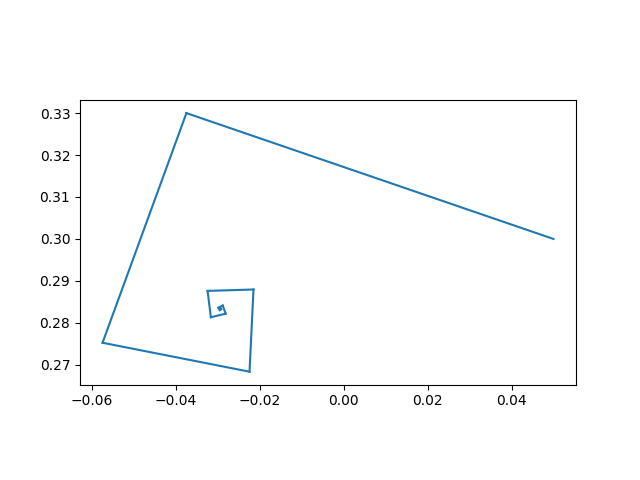
接下来,让我们从橙色圆盘中周期为 2 的点开始。
绘图迭代(-1 + 0.2j)
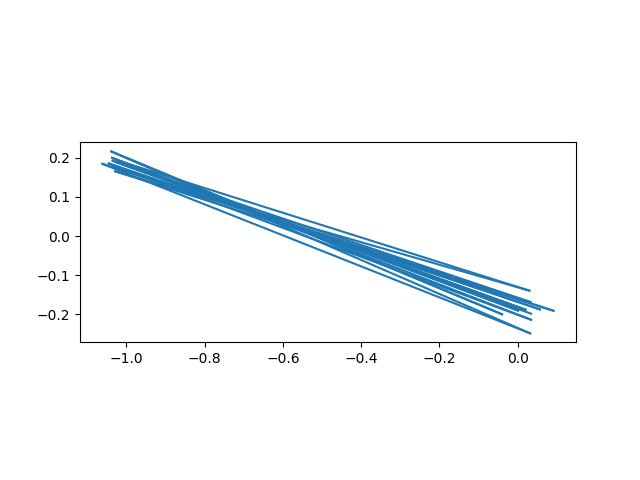
我们可以找到任意周期为n 的点。这是周期为 3 的点。
绘图迭代(-0.13 + 0.66j)
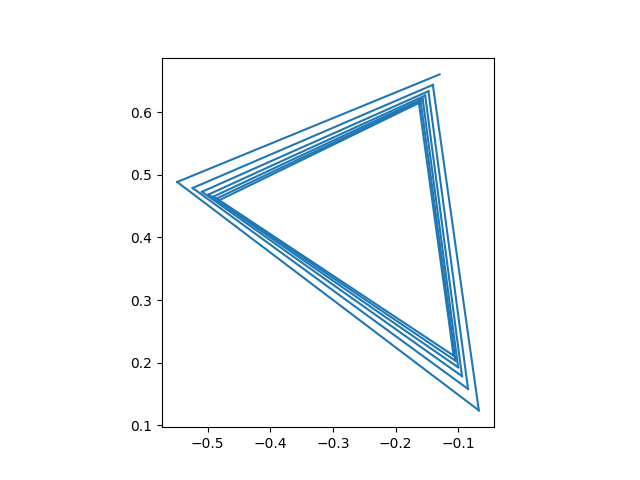
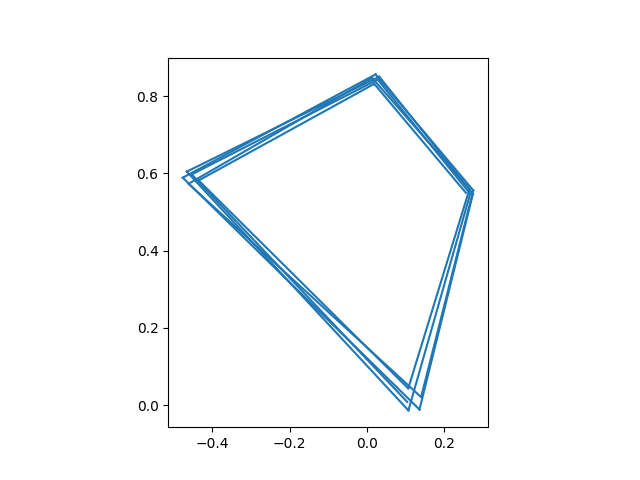
这是第 4 阶段之一。
绘图迭代(0.256 + 0.55j)
收敛到周期为q 的圆的c值是与心形线相切的“球”。共有 φ( q ) 个球,其中 φ 是欧拉函数,即 φ( q ) 是小于 q 且与q互质的正整数的个数。橙色圆盘是第一个球,也是同类中唯一的一个,因为 φ(2) = 1。有两个周期为 3 的球,因为 φ(3) = 2。
对于每个与q互质的p,存在一个球茎与心形线在w (1 − w ) 处相切,其中
w = ½ exp(2π ip / q )
灯泡的直径约为1/ q 。
这些灯泡并不能解释曼德布洛特集合中的所有元素。还有很多东西有待探索。
顺便说一下,这是通过随机选择c的值并测试z ² + c的迭代是否保持有界而创建的曼德布洛特集的图。
各个时期的后曼德布洛点首次出现在John D. Cook身上。
原文: https://www.johndcook.com/blog/2025/09/05/mandelbrot-bulbs/