曼德布洛特和肥尾 – 搞英语 → 看世界

曼德布洛特集是复数c的集合，满足

f （ z ）= z² + c

保持有界。但你怎么知道迭代会保持有界呢？你知道它什么时候会变得无界——如果 | z | > 2，那么点就不会再回来了——但你怎么知道迭代是否永远不会变得无界呢？你不知道。

因此，在实际操作中，绘制曼德布洛特集的软件会迭代最多 5000 次，如果某个点尚未发散，则将其计入集合。为了创建美观的图形，这已经足够了。但如果你想计算曼德布洛特集的面积，这显然不够。

一个合理的做法是观察逃逸时间的分布。然后，你可以说，如果某个迭代在N步之后还没有逃逸，那么它在未来逃逸的概率小于 ε，并且让 ε 足够小以满足计算的精度。

逃逸时间分布一开始下降得非常快，如下图所示。不幸的是，在最初的快速下降之后，它会进入典型的厚尾分布的缓慢下降阶段。这并非罕见：厚尾分布最初的下降速度可能比薄尾分布更快，例如柯西分布与正态分布的比较。

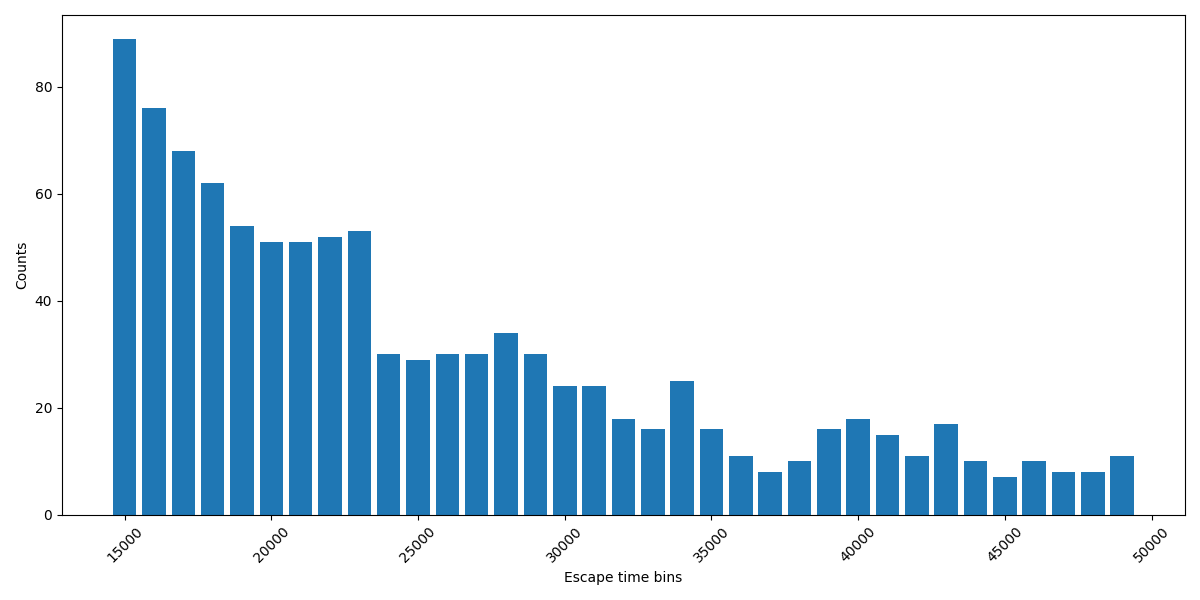
曼德尔布罗特 (mandelbrot) 的胖尾巴

上图将逃逸时间按 1,000 个桶分组。它从最初的快速下降之后开始，并显示了厚尾区域。这是基于 100,000,000 个随机生成的c值得出的。

要估计迭代在保持N步有界后逃逸的概率，你需要知道整个尾部的概率质量。那么，亲爱的读者，上面未显示且未计算的条形面积之和是多少？它不像正态分布，因为你可以相当有把握地说某个点之后的质量可以忽略不计。

这很重要，因为任何绘制曼德布洛特集或估算其面积的程序，其最大迭代次数都在内循环中。如果 5,000 次不够，就使用 50,000 次作为最大值，这会使程序运行时间延长 10 倍。但如果 50,000 次还不够呢？好吧，那就改为 100,000 次，运行时间再次加倍，但这够吗？

也许有人研究过拟合逃逸时间分布，这样就能估算尾部的概率质量。但我只是想玩玩而已，不太了解这方面的文献。我找过相关的论文，但什么也没找到。