
卡尔·布兰登·摩尔维特(1774-1825)设计了一种等积地图投影,将地球表面映射到一个长宽比为 2:1 的椭圆形上。如果您从远处观察地球,您所看到的地球表面将对应于摩尔维特地图中间的一个圆圈。您看不到的地球部分则映射到椭圆形的其余部分。
纬线并非完全等距分布;为了达到相等的面积,需要一定的变形。根据以下公式,纬度φ对应于地图上的θ
θ 作为 φ 的函数,没有闭式解,因此必须进行数值求解。对于每个 φ,我们必须求出
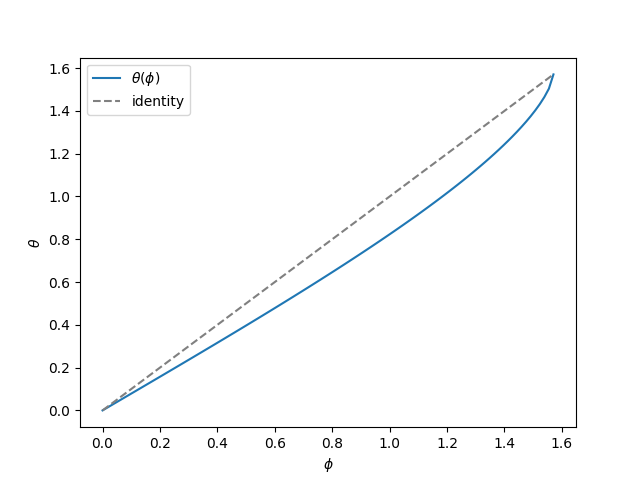
这是 θ 与 φ 函数关系的图。
牛顿法
牛顿法非常有效(平方收敛),除非φ接近π/2。牛顿法在高纬度地区速度变慢的原因是, f及其导数都在π/2处,即f在那里有双重根。
牛顿法在二重根附近从二次收敛减慢到线性收敛,但有一个小的修改可以保持二重根附近的二次收敛。
当m = 1 时,这是牛顿法的通常形式。设置m = 2 可调整二重根法。
当要求的根恰好是二重根时, m = 2 的牛顿法修正版是有效的。但是,如果要求二重根附近的根,设置m = 2 可能会导致方法发散,因此在改变m时必须非常小心。
插图
这是牛顿法的一个版本,专门用于摩尔维特方程。我们可以指定m的值,根的初始估计默认为 θ = φ。
从 numpy 导入 sin、cos、pi def mynewton(phi,m,x0 = None): x = x0 如果 x0 否则 phi 增量 = 1 迭代次数 = 0 当 abs(delta) > 1e-12 时: fx = 2*x + sin(2*x) - pi*sin(phi) fprime = 2 + 2*cos(2*x) 增量 = m*fx/fprime x -= 增量 迭代次数 += 1 返回(x,迭代次数)
远离二重根
假设 φ = 0.25 和m = 1。当我们使用默认初始估计时,牛顿法在 5 次迭代中收敛。
靠近二重根
接下来,假设φ = π/2 − 0.001。我们再次设m = 1,并使用默认的初始估计值。现在牛顿法需要16次迭代。收敛速度较慢,因为我们越来越接近π/2处的二重根。
但如果我们切换到m = 2,牛顿法就会发散。缓慢收敛总比不收敛好,所以我们最好坚持使用m = 1。
关于二重根
现在假设φ = π/2。在这种情况下,默认猜测完全正确,但代码会除以零并崩溃。因此,我们将初始估计值设为π/2 − 0.001。当m = 1时,牛顿法需要15步才能收敛。当m = 2时,它只需6步即可收敛,速度显然更快。然而,这两种情况下,返回的结果都只精确到小数点后6位,而代码要求精确到小数点后12位。
这表明,当我们接近 φ = π/2 时,我们既面临速度问题,也面临准确性问题。
更好的方法
我还没算出来,不过我设想了一下可以解决这个问题。我会调整牛顿法,避免步长过大,这样 φ 在 [0, π/2 − ε] 范围内时就能准确计算;如果 φ 在 [π/2 − ε, π/2] 范围内,我会使用另一种方法,比如幂级数反演。
相关文章
摩尔维特地图投影和牛顿方法一文首先出现在John D. Cook上。
原文: https://www.johndcook.com/blog/2025/09/21/mollweide-newton/