你可能会认为,在更多点上插值会得到更精确的近似值。龙格的一个著名例子证明了事实并非如此。如果在区间 [-5, 5] 上对函数 1/(1 + x ²) 进行插值,随着插值点的增加,最大插值误差实际上会增加。
这是我几年前写的一篇文章中的一个例子,使用了 16 个插值点。这是同一个函数,只是缩放到区间 [-1, 1] 上。
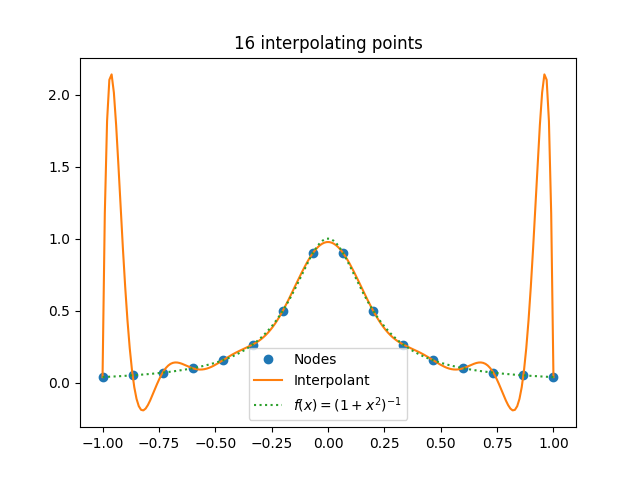
有两件事使得 Runge 的例子有效。
- 插值节点间距均匀。
- 复平面中的奇点太靠近域。
如果使用切比雪夫节点而不是均匀分布的节点,问题就会消失。
如果被插值的函数在单位区间附近的某个区域内具有解析性(详见此处),那么问题也会消失,至少在理论上如此。实际上,使用浮点运算,即使理论上插值函数收敛,你也会看到快速的发散[1]。这就是本文的重点。
例子
让我们尝试在区间 [-1, 1] 上插值 exp(-9 x ²)。该函数处处解析,因此插值多项式应该随着插值点数n趋于无穷大而收敛。以下是n = 50 时的结果图。
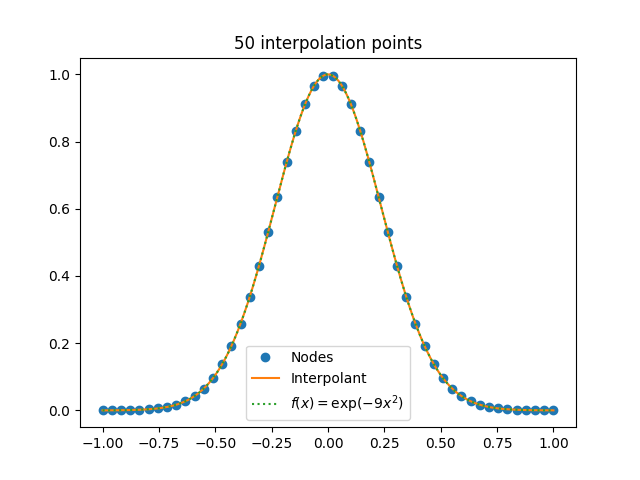
看起来一切正常,不用担心。不过,我们还是试试运气,试试n = 100 吧。
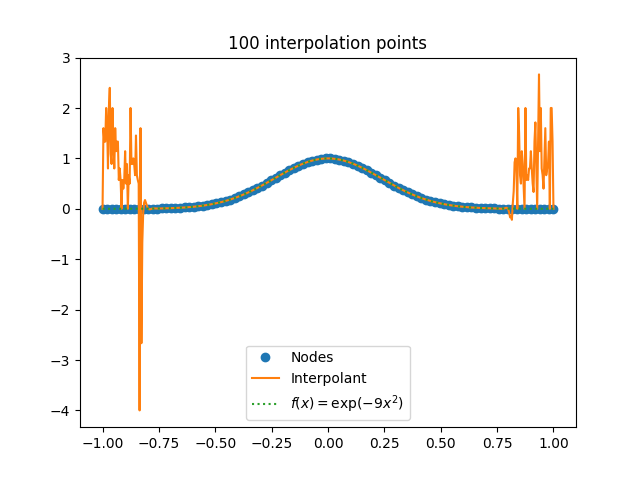
嗯。有点不对劲。
事实上,情况比图表显示的要糟糕得多。最大的插值超过了 7 亿,只是图表上没有显示出来。
在等间距点处进行插值是一种糟糕的条件。如果我们能够以无限精度计算,那就没有问题了,但在有限精度下,插值误差可能会呈指数级增长。
个人轶事
几年前,我了解到有人在一个应用程序中对大量等距点进行 exp(− x ²) 插值。如果我没记错的话,他们想对插值函数进行积分,以便计算概率。
我警告他们,由于龙格现象,这不是一个好主意。
我在理论上错了,因为 exp(− x ²) 是解析的。我不知道龙格收敛定理。
但我从数值角度来看是正确的,因为我也不知道上面展示的数值不稳定性。
所以我犯了两个错误,但它们之间互相抵消了。
相关文章
[1] Lloyd N. Trefethen著《近似理论与近似实践》
文章“插值不稳定性”首先出现在John D. Cook身上。