我们每天看到的图像——无论是印刷品还是显示器——都只是幻象，这一点或许并不令人意外。那张猫图实际上并非一只猫，而是一堆点，当我们从足够远的地方观看时，大脑会误以为我们看到的是一只二维的猫，并欣然填补了空白。这些点可以使用完整的 CMYK 颜色模型（用于印刷品）、RGB(A)（用于数字图像）或包含灰度的有限色彩空间。
或许更有趣的是，抖动技术可以通过添加噪声来进一步欺骗大脑，使其看到原本并不存在的东西。简而言之，抖动就是通过添加噪声来减少量化误差的过程，量化误差在图像中会以色带等伪影的形式出现。在数字音频领域，抖动技术也出于类似的原因被使用。从模拟信号转换为数字信号的过程中，部分过程涉及丢弃超出采样率和量化深度的数据。
通过添加抖动噪声，这些量化误差会被平滑，最终效果取决于所使用的抖动算法。
数字时代
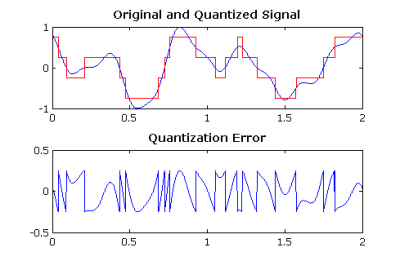量化信号及其误差的图。（来源：维基百科）
在人类历史的大部分时间里，视听记录和再现的方式都是模拟的，始于绘画等方法。直到最近，再现音乐才需要召集技艺精湛的艺术家，直到模拟录音和播放技术的出现。然后，随着20世纪下半叶计算机技术的兴起，我们突然获得了不仅能够进行模数转换，还能以近乎完美的方式存储最终的数字格式的能力。
数字光盘和磁带发现自己正在与诸如盒式磁带和黑胶唱片之类的模拟格式竞争。虽然视频和照片在很长一段时间内都以VHS录像带和胶片的形式保持模拟状态，但最终它们都被数码相机、JPEG、PNG、DVD和MPEG等全数字化格式所取代。尽管理论上数字格式可以实现像素和音符的完美再现，但诸如采样速度（奈奎斯特频率）和前面提到的量化误差等因素意味着一系列新的难题需要解决。
话虽如此，抖动技术的首次应用实际上是在19世纪，当时报纸和其他印刷媒体希望能够打印照片，而无需进行木刻或雕刻的麻烦。这导致了半色调印刷的发明。
波尔卡圆点
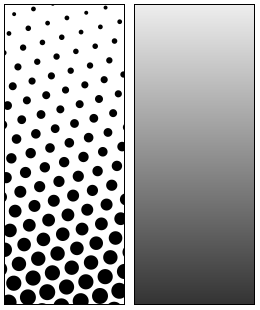左图：半色调点阵图案，尺寸向下逐渐增大。右图：人眼在足够远的距离下看到的景象。（来源：维基百科）
在早期的印刷方法中，插图的油墨覆盖范围仅限于“全有或全无”。这显然意味着，在更精细的插图和照片上，印刷效果会受到严重限制，直到半色调印刷技术的出现。这种方法最初由威廉·福克斯·塔尔博特于1852年获得专利，他使用一种特殊的丝网将图像分解成照相底片上的离散点。将其显影成印版后，这些印版就会印出这种由不同大小的点组成的图案。
尽管在接下来的几十年里，半色调印刷方法的具体细节不断改进，但其基本原理至今依然如故：通过改变网点及其周围空白（白色）区域的大小，感知到的亮度也会随之变化。当这种方法扩展到采用 CMYK 颜色模型的彩色印刷时，由于这三种颜色以相邻的网点形式印刷，即使当时可用的油墨颜色有限，也能在报纸和杂志上印制全彩照片。
虽然也可以使用混合墨水进行 CMYK 打印，例如喷墨打印机，但这也存在一些缺点，尤其是在打印薄而低质量的纸张（例如报纸纸张）时，因为墨水饱和会导致纸张撕裂和变形。因此，CMYK 和单色抖动仍然是报纸和类似低保真应用的常用技术。
调色板
理想情况下，每幅图像的色深都应该不受限制。然而，有时我们不得不适应更窄的色彩空间，例如转换为图形交换格式 ( GIF ) 时，其每像素的位深被限制为 8 位。这种诞生于 1987 年、至今仍非常流行的格式提供了惊人的 256 种可能的颜色——尽管它来自完整的 24 位色彩空间——这在使用 24 位 PNG 或类似格式作为源文件时带来了一些挑战。单纯降低位深会导致严重的色带问题，这意味着我们应该使用抖动来缓解这些急剧的过渡，例如非常常见的 Floyd-Steinberg 抖动算法：
从左到右：原图。转换为网页安全色。使用 Floyd-Steinberg 抖动技术，网页安全色得以保留。（来源：维基百科）
Floyd-Steinberg 抖动算法由 Robert W. Floyd 和 Louis Steinberg 于 1976 年创建。其抖动方法基于误差扩散，即提取导致尖锐条纹的量化误差，并将其分布到相邻像素。这样，即使与原始图像相比，图像质量会明显下降（即出现噪点），过渡也不会那么突兀。
该算法非常简单，每次向下处理一个像素，而不会影响之前处理的像素。获取当前像素的量化误差后，将其分布到当前像素及其下方的后续像素上，如以下伪代码所示：
对每个y从上到下执行 对每个x从左到右执行 旧像素：=像素[ x ][ y ] 新像素：=查找最接近的调色板颜色（旧像素） 像素[ x ][ y ] := 新像素 量化误差：=旧像素-新像素 像素[ x + 1][ y ] := 像素[ x + 1][ y ] + 量化误差 × 7 / 16 像素[ x - 1][ y + 1] := 像素[ x - 1][ y + 1] + 量化误差 × 3 / 16 像素[ x ][ y + 1] := 像素[ x ][ y + 1] + 量化误差 × 5 / 16 像素[ x + 1][ y + 1] := 像素[ x + 1][ y + 1] + 量化误差 × 1 / 16
find_closest_palette_color()函数的实现是这里的关键，对于灰度图像，一个简单的round(oldpixel / 255)就足够了，或者trunc(oldpixel + 0.5)正如威斯康星大学麦迪逊分校 2000 年的 CS 559 课程材料中所建议的那样。
Floyd-Steinberg 算法虽然基础，但由于其只需付出很少的努力就能获得良好的效果，至今仍被广泛使用。但这并不意味着没有其他抖动算法，维基百科中关于抖动的条目很有帮助地指出了许多替代方案，既属于同一误差扩散类别，也属于其他类别，例如有序抖动。在有序抖动的情况下，它呈现出一种独特的交叉影线图案，既非常容易辨认，又可能令人反感。
当然，这里会进行抖动以弥补位深度的不足，这意味着它永远不会看起来与原始图像一样好，但产生的伪影越不令人讨厌，就越好。
音频抖动
虽然乍一看，数字音频的抖动处理似乎与图像的量化误差抖动处理大相径庭，但同样的原理也适用于此。例如，当需要将原始录音下采样至CD质量（即16位）音频时，我们可以对原始样本进行舍入或截断以获得所需的样本大小，但无论哪种方式都会产生失真。由于量化误差会产生新的频率和谐波，人耳对这种失真非常敏感，这在维基百科条目中提供的16位到6位下采样示例中尤为明显。
在抖动处理的样本中，噪声清晰可闻，但原始信号（正弦波）现在听起来非常接近原始信号。这是通过在每个样本中添加随机噪声（随机向上或向下取整并计算平均值）来实现的。虽然最终结果中随机噪声清晰可闻，但它比未抖动的版本明显更好。
图像中也可能存在随机噪声分布，但更精细的方法往往会产生更好的结果。对于音频处理，存在其他噪声分布和噪声整形方法。
无论采用哪种抖动方法，不起眼的印刷机和量化误差如何催生出如此多不同的方法来欺骗人眼和耳朵，使其接受低保真度的内容，这仍然令人着迷。由于抖动技术诞生之初存在的许多技术限制（例如昂贵的存储空间和较低的带宽）如今已基本消失，观察抖动技术在未来几年乃至几十年内的应用将如何演变，将会非常有趣。
特色图片：“JJN Dithering”来自[Tanner Helland]的精彩犹豫文章。
原文： https://hackaday.com/2025/07/09/dithering-with-quantization-to-smooth-things-over/