如果三个圆都相切,你就能找到另外两个与这三个圆都相切的圆,而寻找这两个新圆的方程式非常优雅。这就是笛卡尔定理。
两个相切圆
为了说明笛卡尔定理,我们首先需要三个相切的圆。画两个相切的圆很容易。我们选择坐标系,使第一个圆的中心位于原点
O1 = ( x1 , y1 ) =(0,0)
第二个圆的圆心在x轴上。如果两个圆的半径分别为r 1和r 2 ,则第二个圆的圆心位于
O2 = ( x2 , y2 )= ( r1 + r2,0 ) 。
我假设第二个圆在第一个圆的外面。你可以让一个圆与另一个圆相切,但为了说明笛卡尔定理,我们需要外切圆。
三个相切圆
现在我们取第三个圆的半径为r 3 。这个圆的圆心必定属于以O 1为圆心、半径为r 1 + r 3的圆,以及以O 2为圆心、半径为r 2 + r 3的圆。我之前已经讨论过如何在这里找到两个圆的交点。
为了说明,我选择r 1 = 2, r 2 = 1, r 3 = 2.8。使用上述帖子中的代码,我发现
( x 3 , y 3 ) = (2.93333333 3.79941516)
这是一个情节。
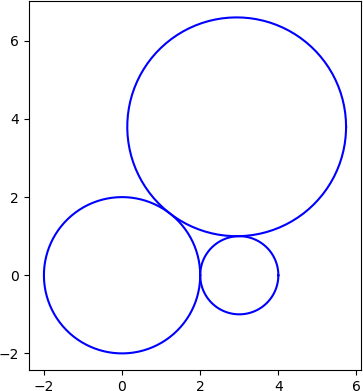
四个相切圆
现在我们可以陈述并说明笛卡尔定理了。这个定理最容易用有符号曲率来表述。
半径为r的圆的曲率为1/ r 。圆大曲率小,圆小曲率大。
对于笛卡尔定理,我们需要使用有符号曲率,如果圆外切,则符号为正;如果圆内切,则符号为负。我们三个圆的有符号曲率均为正,即
k i = 1 / ri
对于i = 1、2 和 3,但笛卡尔定理会给我们两个圆,一个在三个给定的圆之间,一个围绕着它们,分别对应k 4的一个正解和负解。
寻找半径
现在我们可以陈述笛卡尔定理[1]:
( k 1 + k 2 + k 3 + k 4 )² = 2( k 1² + k 2² + k 3² + k 4² )
这给出了k 4的二次方程,它有两个解:
k 4 = k 1 + k 2 + k 3 ±2( k 1 k 2 + k 2 k 3 + k 1 k 3 ) ½ 。
寻找中心
现在我们知道了相切圆的半径,但不知道圆心。为此,我们将圆视为位于以z i为圆心的复平面上。这样,圆心满足的定理与曲率满足的定理类似。
( k 1 z 1 + k 2 z 2 + k 3 z 3 + k 4 z 4 )² = 2( k 1 ² z 1 ² + k 2 ² z 2 ² + k 3 ² z 3 ² + k 4 ² z 4 ²)
我不太清楚这其中的历史,但我不相信笛卡尔有圆心公式。他肯定没有用复数写出上面的公式[2]。
这是笛卡尔定理保证的两个圆的图。
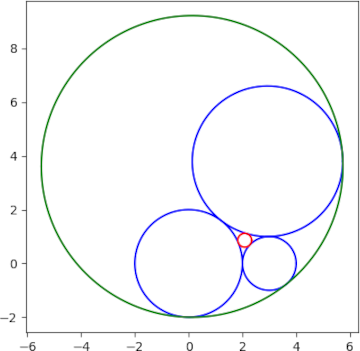
[1] 索迪-戈塞特定理将笛卡尔定理推广到 ℝ n中的n + 2 个球面的情况。曲率和的平方等于n曲率和的平方。
[2] Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks. 超越笛卡尔圆定理。https://ift.tt/MbOiEZA
寻找切线圆一文最先出现在John D. Cook上。
原文: https://www.johndcook.com/blog/2025/07/31/finding-tangent-circles/