今天早上我写了两篇不相关的博客文章,一篇关于数学论文H = W ,另一篇关于将数字放入 D&D对齐矩阵的笑话。
我使用 Grok 查找了 H = W 论文的参考文献,并确认比对矩阵源自《龙与地下城》[1]。我提出新问题时并没有开启新的聊天,但 Grok 觉得有义务将这两个问题联系起来。在回复我的 D&D 问题接近尾声时,Grok 添加了“与 Sobolev 空间查询的联系”一节,内容如下:
虽然对齐系统和索博列夫空间(源自您之前关于“H = W”论文的疑问)在数学上毫无关联,但它们都体现了为复杂系统创建结构化框架的努力——对齐系统用于性格伦理,索博列夫空间用于函数分析。“中性”对齐,如同分布的规律性,代表一种平衡或中间状态,连接着两个极端(规律/混沌,或规则/奇异分布)。
原文中强调。
一方面,这简直是无稽之谈。另一方面,索博列夫空间和 D&D 对齐矩阵是复杂系统的结构化框架!
Grok 的回应让我想起当我在学习时打瞌睡时,我的大脑会在我所学的一切之间找到奇妙的荒谬联系,例如整合法语动词的方式。
对齐功能
将功能归类到 D&D 阵营网格中似乎有些愚蠢,但如果我们非要这么做呢?以下是我的一些想法。
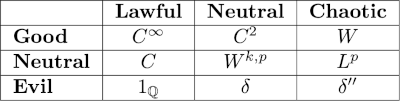
良函数和守恒函数都有经典定义。C 是连续函数空间, C ² 是具有两个连续导数的函数空间, C ∞是无限可微函数空间。
被归类为混沌善的函数W是魏尔斯特拉斯的无处可微、处处连续函数的例子。
真正的中立函数W k , p (与魏尔斯特拉斯函数 W 无关)是之前文章中的索博列夫空间。k 越大,函数越正则。L p是W k , p,其中k = 0。这些函数不一定是逐点定义的,而只需对测度为零的集合进行模运算即可。
函数 1 ℚ是有理数的指示函数,即,如果一个数是有理数,则该函数等于 1,如果一个数是无理数,则该函数等于 0。
这里δ是狄拉克函数δ,δ是它的n阶导数。这是一个广义函数,而不是任何经典意义上的函数,对其求导只会使其变得更糟。
[1] 1974 年版的 D&D 原版只有一个轴心:守序、中立、混乱。1977 年,游戏增加了第二个轴心:善良、中立、邪恶。
复杂系统的结构化框架一文最先出现在John D. Cook身上。