埃尔多斯-莫德尔三角定理 – 搞英语 → 看世界

如果说有哪个数学领域被彻底梳理过的话，那就是欧几里得几何。但偶尔有人会提出一个新定理，看起来它应该在几个世纪前就被发现了。

这是 Paul Erdős 在 1935 年猜想的定理，并于同年晚些时候由 Louis Mordell 证明。

如果从给定三角形ABC内的点O垂线OD 、 OE 、 OF绘制到其边上，则

OA + OB + OC≥2 ( OD + OE + OF )。

当且仅当三角形 ABC 是等边时，等式成立。

更简洁地说，

从任何内部点开始，到顶点的距离至少是到边的距离的两倍。

这是一个例子。在上图中，定理表明蓝色虚线加在一起的长度是红色实线的两倍多。

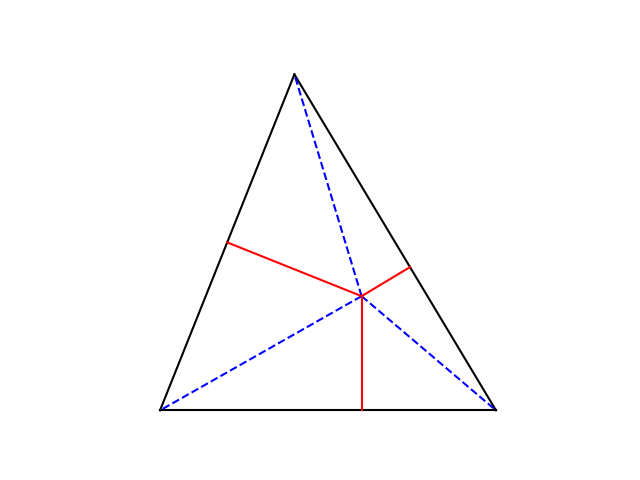
在我绘制上图时使用的单位中，蓝线的总长度为 9.5，红线的总长度为 4.7。

Hojoo Lee 在 2001 年给出了 Erdős-Mordell 定理的基本证明，该证明大约需要一页纸的打印量 [1]。

在我看来，埃尔多斯-莫德尔定理就像是古代几何学家可以发现并证明的定理。这是该定理的概括，感觉更加现代 [2]。

设R _i为从内点O到第 i个顶点的距离， ri_为到第 i个顶点相对侧的距离。令λ ₁ 、λ ₂和λ ₃为任意三个正实数。然后

$\sum_{i=1}^3 \lambda_iR_i \geq 2\sqrt{\lambda_1\lambda_2\lambda_3} \sum_{i=1}^3 \frac{r_i}{\sqrt{\lambda_i}}$

当所有的 λ 都等于 1 时，我们得到原始的 Erdős-Mordell 定理。

您可以说到顶点的加权距离至少是到边的加权距离的两倍，但您必须更多地谈论权重，并且一般来说，权重在不等式两边的作用不同。

[1] 李浩珠. Erdős-Mordell 定理的另一个证明。几何论坛，第 1 卷 (2001) 第 12 页7–8

[2] 西尼·达尔，谢伊·格隆。加权 Erdős-Mordell 不等式。美国数学月刊。卷。 108，第2号，2001年2月

后埃尔多斯-莫德尔三角定理首次出现在约翰·D·库克 (John D. Cook)身上。

原文： https://www.johndcook.com/blog/2025/04/13/erdos-mordell/