勒让德多项式 – 搞英语 → 看世界

上一篇文章提到了勒让德多项式。这篇文章将简要介绍这些多项式，并提供一些它们在实际应用中的技巧。

定义勒让德多项式的一种方法如下。

中间的要点意味着

$\int_{-1}^1 P_m(x) P_n(x) \, dx = 0$

如果m ≠ n 。每个P _k都与其前一个 P k 正交的要求决定了P _k最多为一个常数，而条件P _k (1) = 1 决定了该常数。

这是前几个勒让德多项式的图。

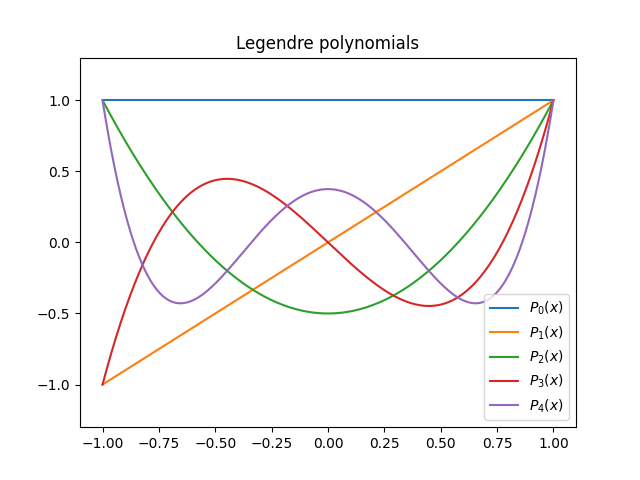
当你绘制大量勒让德多项式时，像上图这样的图表的空白处会出现一个有趣的模式。请参阅这篇文章。

勒让德多项式P _k ( x ) 满足勒让德微分方程；这就是他们的动机。

$(1 - x^2) y^{\prime\prime} -2x y^\prime + k(k+1)y = 0$

这个微分方程出现在球谐函数的背景下。

接下来我将描述勒让德多项式的几何原理。假设有一个三角形，其中一条边的长度为单位，另外两条长边的长度分别为r和y 。

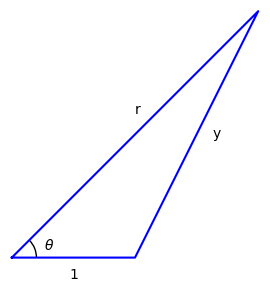
你可以利用余弦定律，根据r找到y ：

$y = \sqrt{1 - 2r \cos \theta + r^2}$

但是假设你想用 1/ r的级数来表示 1/ y 。（这看起来像是一个任意的问题，但它在应用中会出现。）那么勒让德多项式就能给出该级数的系数。

$\frac{1}{y} = \frac{P_0(\cos\theta)}{r} + \frac{P_1(\cos\theta)}{r^2} + \frac{P_2(\cos\theta)}{r^3} + \cdots$

资料来源：Keith Oldham 等人。功能图集。第二版。

勒让德多项式一文最先出现在John D. Cook身上。

相关文章