你住在沙漠里！

月亮塔 #240

克里斯·阿卜杜勒梅西 9月8日

在应用程序中阅读

朋友们，

我们从一个抓包开始。

1) 省钱秘诀：检查一下您支付的汽车保险费用。

显然，对于那些应该具有竞争力和商品化的东西来说，存在着很大的分散性。我的全州续约即将到来。它看起来像是赎金而不是账单。我通过 Geico 的自动报价生成器运行了相同的承保详细信息，而且价格便宜 1/3。我正在通过经纪人收集更多报价，因此我不会向 Geico 支付先令。只是提醒一下，就像有线电视公司一样，许多公用事业类企业对待现有客户的态度比潜在客户更差。这就像对待你的伴侣比对待一个可爱的咖啡师更糟糕。糟糕的形式。

2）家长读者经常问我为孩子们做什么活动。我们为数学所做的事情……

去年，五年级时，扎克自学了“ 解决问题的艺术”课程。每周大约 5 个小时，花费了整个学年的时间。我真的很喜欢这个课程，他也很努力地完成它……但他没有参与社区，所以感觉太像纸牌游戏了。我觉得他不会太兴奋再做一年，特别是当他适应六年级并且有更完整的运动日程时。俄罗斯数学和公共文式比较费劲，不那么专注于文字问题和拼图类型的问题，这些问题会让学生感到紧张，但 AoP 太多了。 （我的第一选择伯克利数学圈已经满了）。

我们选择了另一个数学圈风格的项目——emc.school 。每周承诺 2 小时的 Zoom 直播，由一名教练和最多 6 名孩子组成的班级进行。如果概念需要更多的练习，还有每周的家庭作业和额外的练习。有一个 1 小时的免费评估，让您对材料有一个很好的了解，并指导您的孩子进入哪门课程。

现在推荐还为时过早，但他已经度过了整整一周，而且课程很扎实。即使已经过了 3 周，您也可以随时加入。我只是想分享我们为关心的人所做的事情。

[顺便说一句，原则上我不是公文式的粉丝，但我三年级的学生马克斯刚刚加入了它，因为他想加入他的一位好友，他认为他擅长数学。此外，我们最近对马克斯有了很多了解，因为他正在经历一个有趣的成长时期，其中有一些因素在起作用。尽管我总体上持保留态度，但公文式的事情感觉就像是我们正在沉迷的一种实验。如果说作为父母你要学到一件事的话，那就是让你的孩子与能够解锁他们的事物相匹配需要开放的心态。我曾经向我的妻子强烈反对公文式，这个孩子让我开始质疑自己。我们将看看事情进展如何。]

3) 几周后我将在我的乐队班上演奏一套。我们的曲目列表中听起来最好的歌曲是 Fleetwood Mac’s Dreams 。如果你的年龄只有我一半，你可能知道这首歌是 Ocean Spray 蔓越莓汁歌曲。不管怎样，这首歌听起来很杀手，因为我们的歌手凯瑟琳。在我们的乐队聊天中，她分享了玛丽·斯彭德解释这首歌的故事的这段精彩视频。这个视频的内容很棒，但格式超级新鲜。我从来没有见过这样的事情：

关于《Dreams》的一个有趣的事实是，它是 A 小调，但 A 小调和弦在整首歌中只演奏了一个小节。

4) Spender 的视频很漂亮，但我们也会选择一些粗糙的东西。一个永远能杀死我的人。我会在序言中说，如果声音恰到好处，我完全是喜剧咆哮的傻瓜。弗兰克·科斯坦萨 (Frank Costanza)、格雷格·吉拉尔多 (Greg Giraldo)、唐·“DC”·库里 (Don “DC” Curry)、丹尼斯·利里 (Denis Leary)、比尔·伯尔 (Bill Burr) 和这个：

我不想用“内容大脑”来玷污这个笑话，但我无法控制自己。 “你住在沙漠里！”这是习得性无助的一个非常好的比喻。你不能告诉我，你的生活中没有一个闷闷不乐的抱怨者，你不想对他们尖叫这句话。

像这样的咆哮对我来说是一个令人鼻孔苏打的作弊代码。就像动物说话的电视广告或任何极其尴尬的拉屎故事（这也是包含我听朋友讲过的最好故事的类别……我们想用它制作一个动画短片。我一想到就快死了它）。我的大脑中有些东西无法抗拒这种幽默。

[关于我的一件可笑的事，我的家人都非常清楚，那就是我是一个多么无助的气喘吁吁，有时甚至近乎无声的窒息，笑哭的人。如果你让我走，你自己就会死。]

金钱角度

我会做更多的一件事是分享我对读者问题的回答。这是一个当期权投资者了解偏差时永远困惑的话题（强调我的）：

在您出色的文章《 0.50 Delta 期权的教训》中，您写道，通过提高看跌期权偏差，市场使看涨期权价差变得更加昂贵。结合您对垂直价差、隐含分布的深入理解以及将价差视为赔率的见解，我想知道倾斜的陡度与直接买入或卖出期权有何关系。

我的问题是：假设 SPX 12 月 24 日看涨期权偏差（100-105 货币性）正在下降。如果我以 100/105 的货币价值购买看涨期权价差，我可能会认为它比 100/95 的看跌期权价差稍贵一些。这与您一直在写的内容一致。然而，我不明白的是：如果看涨期权价差更贵（因为105 vol低于ATMF），那么由于波动率低，直接购买105看涨期权不是更好吗？在我看来，这与我们从利差中得到的看法相矛盾。市场似乎倾向于上涨的情况并推高看涨期权利差，但与此同时，直接看涨期权变得更便宜？

这可能与 IV、Delta 或 VRP 有关吗？

这是一个非常重要且常见的问题。

我的回应：

我知道这感觉很矛盾。我什至这样设计它，因为它吸引了你的注意力……感觉真的很像！

但最终并非如此。

考虑一下期权偏斜产生的垂直价差价格意味着“纠正”布朗运动假设的分布，即市场呈正偏斜，但更有可能下​​跌而不是上涨。

这与实证结果完全相反……市场呈负偏态，有望上涨！

上行看涨期权更便宜，因为正长尾偏斜比布莱克斯科尔斯假设的要小，但看涨期权价差更昂贵，因为股票更有可能上涨。

我们将概率向右移动，但截断了上行的幅度。这就像押注于体育运动中的最爱……你可能是对的，但好处并不大。

要点是，分布就像一个雕塑——波动性偏斜将一些粘土从右尾移动到左尾，并使整个雕塑向右移动一点。

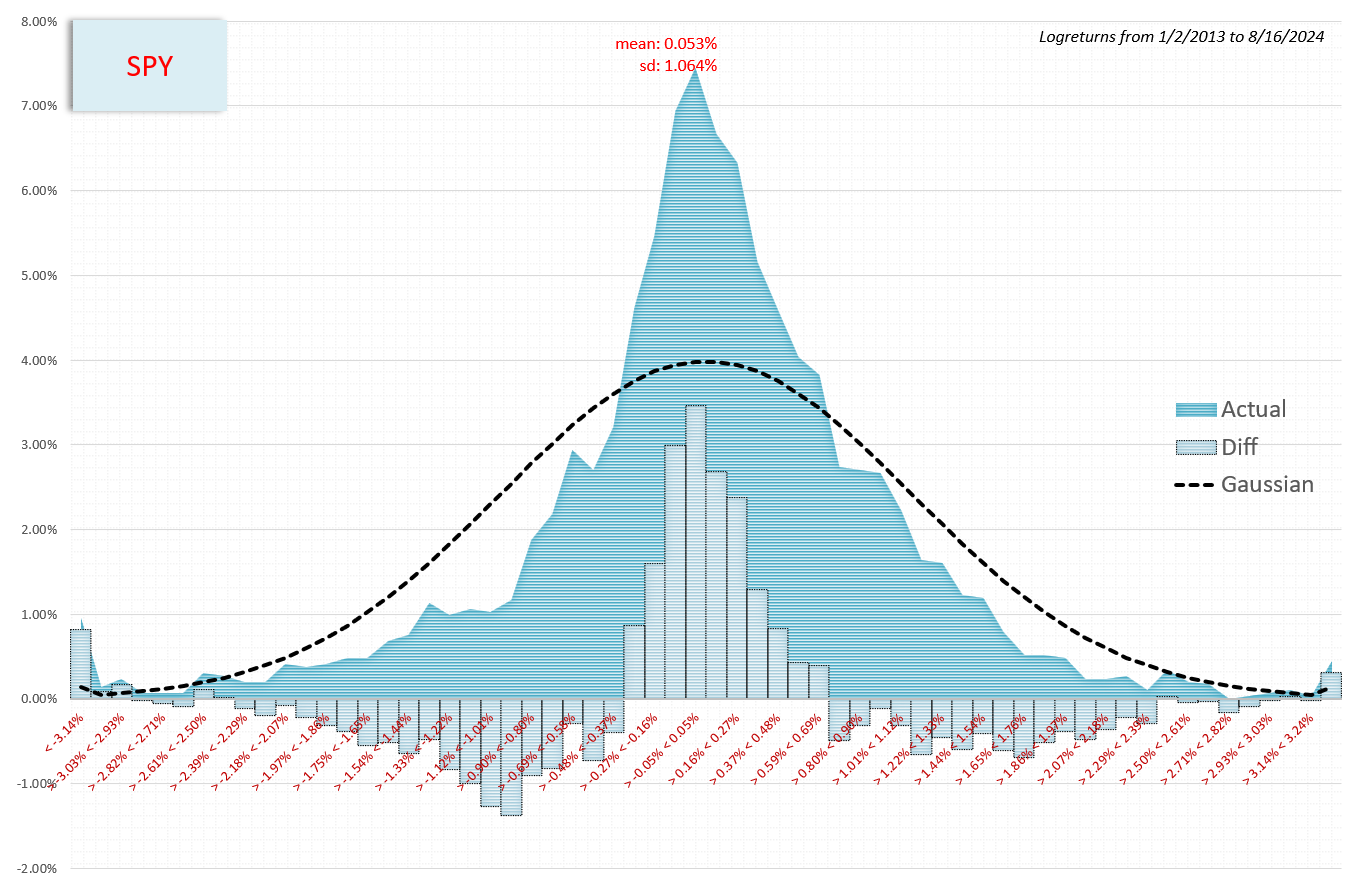
受虐狂的金钱角度

周四 Moontower 的付费帖子通常会更深入地探讨实际的投资概念。他们最近非常以选择为中心。然而，我最近写的最受欢迎的一篇文章并不直接涉及期权。它带动了 20 名付费潜艇，这是一个异常高的数字。

[顺便说一下，我很乐意讨论付费墙、货币化等话题。事实上，我有一个积压的项目来提出“我是否应该付费墙内容”的定价模型，主要是为了逐项列出此类模型的大部分主要输入及其敏感性或希腊语。无论如何，至少从我的角度来看，货币化话题似乎没有得到充分讨论。我想知道这是否是因为人们不愿意分享。无论如何，我认为在如何考虑货币化方面不透明没有任何好处。归根结底，我写的一些内容是付费的。我付出了很多努力，但我不认同马克思的劳动价值论——如果值得付出代价，就会得到报酬，如果不值得，就不会得到报酬。]

这是帖子，付费专区已被删除?

? 波动性取决于分辨率

尽管标题中有“波动性”一词，但它与风险主题的关系比期权更广泛。这篇文章不长，但对任何投资者来说都有很多值得思考的地方。它的核心可以概括为一句话：

实际波动率取决于采样频率

这个概念具有如此广泛的吸引力，并且由于我在《金钱角度》中关于实现分布与理论对数正态分布的部分内容，它似乎是一个值得解锁的好概念。

子堆栈帖子是整个帖子的浓缩版本，其中包含大量图表。

例如，比较实际每日回报与理论预期回报的图表：

现实世界的分布包括：

1. 更肥的尾部（请注意，大于 3 st devs 是一个巨大的桶，所以这就是为什么即使是高斯期望也会向后倾斜一点）

2. 更高的峰值（比理论预测更多的小幅波动）

3. 正漂移（理论上，漂移约为 [RFR-div 收益率]/365……比实际漂移小得多。顺便说一句，人们确实很难接受 Black-Scholes 假设，即股票没有预期回报溢价 – 但是这实际上不是一个假设，除非你谈论的是一个特定的背景——作为复制投资组合的定价选项对此有一个很好的澄清。）

期权市场通过以下方式适应这一经验现实：

1. 增加下行看跌期权 IV 或看跌期权偏斜。这扩大了左尾的分布，但也通过推高 ITM 看涨期权的价值和看涨期权价差，增加了股票正回报的隐含概率。这会将分布的中心向右移动。

2. 看涨期权和看跌期权的侧翼期权可以增加尾部的质量。在价格空间中，这会推高 OTM 期权相对于 ATM 跨式期权的价值，从而增加蝴蝶的价值（翅膀向上，相对于苍蝇的“肉”）。如果您认为股票将会有更多如果波动比对数回报的高斯分布预测的小，那么您想购买做空 ATM 跨式期权的蝶式期权——这正是价值增加的结构。

波动率偏差产生了符合经验精算赔率的期权价差价格。他们“纠正”了基本布莱克-斯科尔斯分布中的假设。

这次谈话中最具争议性的兔子线索之一是，对于一个假设回报率较高的投资者来说，使用 RFR 进行漂移定价的长期看涨期权价格看起来非常便宜（而看跌期权则昂贵），因为该股票的回报率较高。有风险。但如果他们根据模型中的回报假设买入看涨期权并提供看跌期权，他们将为期权交易者提供无风险套利利润，而他们只需执行“转换”策略即可。*

如果这引起您的兴趣，请查看现实世界与风险中性世界中沃伦·巴菲特的部分。

*转换示例

股票 = 100 美元

利率=3%

合成期货的 Theo 价值（即多头 100 份行使权看涨期权/空头 100 份行使权看跌期权）= 103 美元

看涨期权的价值将比看跌期权的价值高 3 美元。 C – P = 3 美元。

买入看涨期权并卖出看跌期权与“以 3 美元买入 100 次执行组合”相同，相当于以 103 美元买入合成期货 – 为什么？无论您在一年内行使看涨期权还是获得看跌期权，您都将为股票支付 100 美元。另外，您今天为该结构支付了 3 美元，这就是为什么您可以说您为一年内结算的股票支付了 103 美元。

想象一下，一位基本面投资者认为该股票一年后价值 108 美元（8% RoR，而不是 RFR），并愿意为该组合支付 5 美元，即 105 美元购买该股票的 1 年期期货。

他们将被套利交易者埋葬，他们会以 5 美元的价格出售该组合，并以 100 美元的价格购买股票以进行对冲。到期时，套利者将被指定做空看涨期权或行使其多头看跌期权，保证他们以 100 美元的价格出售股票。他们今天已经以 100 美元的价格购买了该股票，并且需要支付 3 美元的利息才能持有该股票一年。因此，在到期时，他们会将股票交付给基本面投资者（以 100 美元的价格出售他们以 100 美元购买的股票……一次清洗）。

套利者将支付 3 美元的利息……但请记住，他们通过组合收取了 5 美元的期权费。最终结果：2 美元无风险利润

市场吸纳了无风险利润，因此套利者将竞相将组合价格一路压低至 3 美元出售给基本面投资者，与 RFR 相比，组合价格相当合理。

基本面投资者或沃伦·巴菲特的想法并不重要。如果他们支付的看涨期权相对于看跌期权的费用高于套利权证的成本，他们就会获得套利。这与股票分布、波动性或任何理论书呆子的东西无关。一个 10 岁的孩子可以通过“转换”套利提取现金流。

“逆转”套利则相反……如果组合太便宜，比如 1 美元，您可以购买合成期货（买入看涨期权/卖出看跌期权），做空股票，到期时您的空头股票将被您购买的股票覆盖通过期货（即行使多头看涨期权，或在看跌期权上获得分配），您从空头股票收益中赚取的 3 美元利息涵盖了您为组合支付的 1 美元溢价，留下 2 美元的套利利润。

实际上，逆转和转换（您在期权中了解到的第一个套利交易）仍然存在风险。

• 如果股票在行使价时到期，则存在固定风险，您必须猜测您是否会被分配期权。

• 利率可能会根据您最初的假设发生变化——您为多头股票支付的隔夜利率或作为空头回扣收取的隔夜利率会发生变化。如果股票变得难以借入，它们也可能发生巨大变化。

• 股息可以宣布、增加或减少。较高的股息会增加看跌期权相对于看涨期权的价格，因此，如果您有反转头寸并且股票宣布股息，您的多头组合将因股息而下降

• 换句话说，反转头寸是多头 rho，转换是空头 rho（它是利率下降、股票变得难以借入或股票支付更大股息的根源）

保持时尚

☮️

月亮塔每周回顾

• 没有被摘下

• 衍生品“收入”大肆狩猎

推荐朋友

需要帮助分析业务、投资或职业决策吗？

跟我预约电话吧

60 分钟 500 美元。让我们一起解决您的问题。如果您不满意，您将获得退款。

让我知道您想讨论的内容，我会在聊天之前直接回答您是否可以提供帮助。

我是在 2022 年初通过读者的入站询问偶然开始做这些事情的。所以我通过 Substack Meetings 测试版挂出了一张牌。您可以看到我如何帮助他人：

?预约会议

网络上的月亮塔

? 所有 Moontower 元博客文章
? 关于我

具体的月亮塔项目

? 月亮塔金钱
? MoontowerQuant
? 肯定句和北极星
? Moontower Brain-插件

策展

✒️ Moontower 其他人最喜欢的帖子
? 我喜欢的阅读指南
?️ 我读过的投资博客
? 儿童书籍创意

乐趣

?️ 月塔音乐
? 月亮塔鸡尾酒
?月亮塔棋盘游戏

升级

赠送订阅礼物

团体订阅可享受 20% 的折扣

© 2024克里斯·阿卜杜勒梅西赫
1212 百老汇广场套房 2100, 核桃溪, CA 94596
退订