β分布是二项式似然函数的共轭先验,因此后验概率的计算非常简单:只需将数据添加到分布参数中即可。假设你从比例为θ的β(α, β)先验分布开始,然后观察到s次成功和f次失败,则θ上的后验分布为
β(α+ s ,β+ f )。
后台正在进行积分,但你无需思考。如果使用其他先验知识,就必须计算积分,而且积分形式并不简单。
先验分布参数之和 α + β 被解释为先验中包含的观测值数量。例如,beta(0.5, 0.,5) 先验不提供信息,其信息量仅相当于一个观测值。
我昨天一直在思考这些,因为我正在做一个项目,客户认为比例θ在0.9左右。一个合理的先验分布是beta(0.9, 0.1)。这样的分布均值为0.9,信息量不大,但对于我设想的用途来说,它完全没问题。
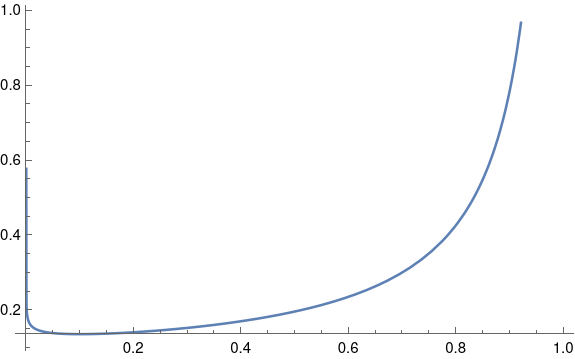
非信息性 beta 先验在实践中效果很好,但如果将它们绘制成图,就会有点令人不安。你会注意到 beta(0.9, 0.1) 的密度在区间 [0, 1] 的两端都存在奇点。右端的奇点还不算太糟,但奇怪的是,一个设计为均值为 0.9 的分布在 0 处密度却无限大。
如果你更进一步,使用一个完全没有信息量、不恰当的 beta(0, 0) 先验,那么在区间的两端都会出现强奇异性。然而,这在实践中并非问题。未用贝叶斯术语表达的统计运算通常等同于像这样带有不恰当先验的贝叶斯分析。
这就引出了两个问题。为什么非信息先验必须将无限密度置于某个地方?为什么这不是问题?
参数较小的β密度函数存在奇异性,因为这只是β函数家族的局限性。如果你使用严格主观的贝叶斯框架,你不得不说,这样的密度函数与任何人的主观先验都不匹配。但正如本文开头所解释的,β分布使用起来非常方便,所以每个人都会做出一些意识形态上的妥协。
至于为什么奇异先验不成问题,可以归结为密度和质量之间的差异。beta(0.9, 0.1) 分布在 0 点处密度无穷大,但在 0 点处质量却不大。如果在小区间内对密度进行积分,会得到一个很小的概率。上图中左侧的奇点很难看清,几乎是一条与纵轴重叠的垂直线。因此,尽管曲线垂直,但曲线下方的面积并不大。
你不可能总是得到你想要的东西。但有时你会得到你需要的东西。
相关文章
文章《你不可能拥有你想要的一切:测试版》最先出现在John D. Cook 的博客上。